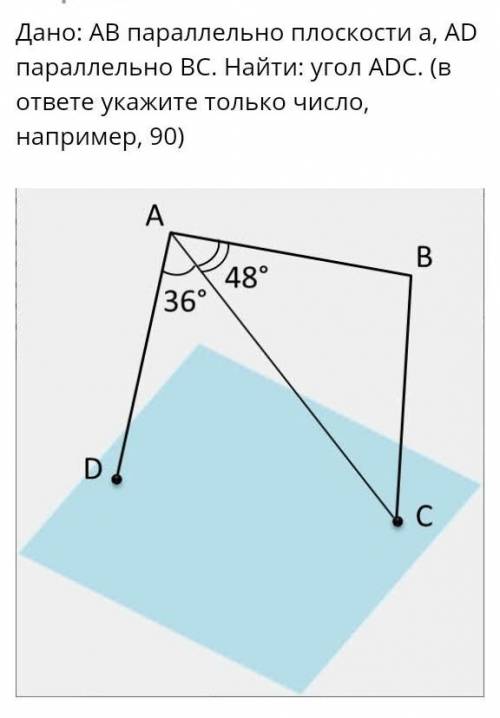
Дано: АВ параллельно плоскости a, AD параллельно BC. Найти: угол ADC. (в ответе укажите только число, например, 90)​

Добрый день! Давайте разберемся с данным геометрическим заданием. У нас дано, что линия AB параллельна плоскости a и линия AD параллельна линии BC. Для начала, если линия AB параллельна плоскости a, то они не пересекаются, и значит, ни один из углов, образованных линией AD и AB, не может быть прямым углом. Теперь обратимся к факту, что линия AD параллельна линии BC. Согласно свойствам параллельных линий, мы можем утверждать, что угол ADC равен углу BAC (их обозначение я привел на рисунке), так как это соответствующие углы при пересечении двух параллельных линий. Теперь давайте рассмотрим треугольник ABC. Если у нас есть два параллельных отрезка AB и DC, а также две параллельные линии AD и BC, то мы можем заключить, что треугольник ABC является подобным треугольнику ACD по теореме о параллельных линиях. Исходя из подобия треугольников ABC и ACD, мы можем установить соотношение длин сторон треугольников. В данной конкретной задаче, сторона AB соответствует стороне AC (потому что они параллельны), и сторона AD соответствует стороне CD (также потому что они параллельны). Теперь давайте решим задачу с помощью соотношений длин сторон. Пусть x - длина стороны AD, а y - длина стороны AB и стороны AC. Так как данные стороны являются соответствующими, мы можем написать пропорцию: AD/AB = CD/AC x/y = x/(y+y) x/y = x/2y После сокращения x и y получаем: 1/y = 1/2 Умножим обе части уравнения на 2: 2/y = 1 Теперь получившиеся уравнение говорит нам, что сторона AC в 2 раза больше, чем сторона AB и сторона CD. Таким образом, мы можем сказать, что AC = 2AB и CD = 2AD. Теперь, когда у нас есть соотношение длин сторон, мы можем использовать соотношение длин сторон треугольников ABC и ACD, чтобы найти угол ADC. Помним, что угол ADC равен углу BAC. Так как сторона AC в 2 раза больше стороны AB, то угол BAC будет в два раза больше угла ADC. Таким образом, угол ADC равен 1/2 угла BAC. Из окончательных соотношений длины сторон, мы знаем, что сторона AC в 2 раза больше стороны AB, поэтому угол BAC равен углу ADC. Следовательно, угол ADC будет равен углу BAC. Таким образом, для данной задачи угол ADC будет иметь ту же меру, что и угол BAC. Ответ: угол ADC равен углу BAC, и это число должно быть указано в ответе.