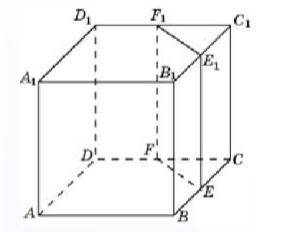
Дано: ABCDA 1 B 1 C 1 D 1 – куб с ребром 10 см. Точки F, F 1 , E 1 , E –
середины ребер DC, D 1 C 1 , B 1 C 1 , BC
соответственно.
Найти: площадь четырехугольника
FF1E1E.
Другие вопросы по теме Математика
Популярные вопросы
- Суретке қарап мәтін құрау. 5-6 сөйлем...
1 - За якими правилами жили слов яни до Руської правди...
2 - Виконай віднімання 4- 10/11...
1 - Коливальний контур генератора радіохвиль містить котушку індуктивністю 48 мкГн,Яку...
2 - Шығарма үзінділерінен шылауларды тауып, өзі тіркескен сөздермен жазыңдар. Олардың...
1 - Скласти план до теми Життя Гобсека , за повістю Оноре де Бальзак Гобсек...
2 - Хелп ми, вообще не понимаю физику:(...
2 - Үйсіндер қандай мемлекеттің ықпалында болды?...
1 - 3. Фигуралардың қабырғаларын өлше. Берілген шаршыданқабырғалары 1 см ұзын шаршы...
1 - Проаналізувати вислів щоб досягти мети потрібно насамперед йти...
3
1. Вначале найдем длины отрезков FE и F1E1.
Отрезок FE является диагональю грани ABCD, и так как ABCD - квадрат со стороной 10 см, то FE также равен 10 см.
Отрезок F1E1 является диагональю грани A1B1C1D1, и так как A1B1C1D1 - квадрат со стороной 10 см, то F1E1 также равен 10 см.
2. Выразим площадь четырехугольника FF1E1E через площадь треугольников FFE и F1E1E.
Площадь четырехугольника FF1E1E равна сумме площадей треугольников FFE и F1E1E:
Площадь FF1E1E = площадь FFE + площадь F1E1E
3. Найдем площади треугольников FFE и F1E1E с помощью формулы площади треугольника.
Площадь треугольника можно выразить через полупериметр треугольника и длины его сторон.
а) Площадь треугольника FFE:
Длины сторон треугольника FFE - FE, FF1 и F1E1.
Найдем полупериметр треугольника FFE: (FE + FF1 + F1E1) / 2 = (10 + ? + 10) / 2 = (20 + ?) / 2 = 10 + ?
Так как треугольник FFE является равнобедренным со сторонами FE и FF1, то его высота HH1 будет перпендикулярна основанию FE, и FE становится базисом или основанием этого треугольника.
Воспользуемся формулой площади треугольника: площадь FFE = (базис * высота) / 2 = (FE * HH1) / 2 = (10 * HH1) / 2 = 5 * HH1
Таким образом, площадь FFE равна 5 * HH1.
б) Площадь треугольника F1E1E:
Длины сторон треугольника F1E1E - F1E1, FE и F1E.
Найдем полупериметр треугольника F1E1E: (F1E1 + FE + F1E) / 2 = (10 + 10 + ?) / 2 = (20 + ?) / 2 = 10 + ?
Так как треугольник F1E1E является равнобедренным со сторонами F1E1 и FE, то его высота HH1 будет перпендикулярна основанию F1E1, и F1E1 становится базисом или основанием этого треугольника.
Воспользуемся формулой площади треугольника: площадь F1E1E = (базис * высота) / 2 = (F1E1 * HH1) / 2 = (10 * HH1) / 2 = 5 * HH1
Таким образом, площадь F1E1E также равна 5 * HH1.
4. Подставим найденные значения в формулу площади FF1E1E.
Площадь FF1E1E = площадь FFE + площадь F1E1E = 5 * HH1 + 5 * HH1 = 10 * HH1
Таким образом, площадь четырехугольника FF1E1E равна 10 умножить на значение HH1.
Для получения конкретного численного значения площади FF1E1E необходимо узнать значение HH1, для чего нужна дополнительная информация или условие задачи. Однако, мы можем дать выражение для нахождения площади FF1E1E без конкретного численного значения:
Площадь FF1E1E = 10 * HH1, где HH1 - высота треугольников FFE и F1E1E, которая зависит от дополнительной информации или условия задачи.