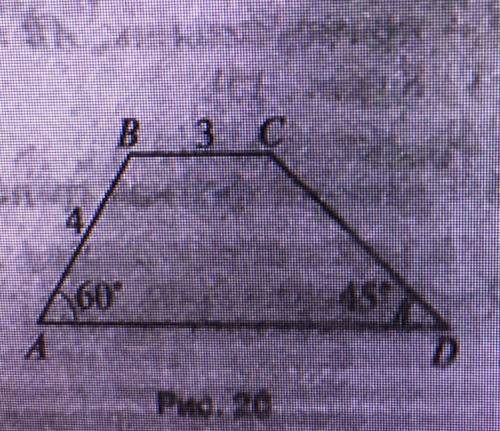
Дано: ABCD - трапеция
Найти: Pabcd, Sabcd
Заранее

Пошаговое объяснение:

Проведем высоту ВН. Получим треугольник АВН, у которого угол АВН=30*. Тогда АН=1/2АВ=4*1/2=2.

Найдем высоту ВН.

ВН^2=FD^2-AH^2=4^2-2^2=16-4=12;

BH=√12=2√3.

Проведем высоту CN. Получим треугольник CDN, у которого угол CDN равен углу NCD и равен 45*. Следовательно треугольник CDN - равнобедренный и CN=DN.  Но CN=BH=√12. Следовательно DN=CN=BH=√12=2√3.

Основание AD=AH+HN+ND=2+3+√12=5+√12.

Найдем сторону CD.  CD^2=CN^2+DN^2=(√12)^2+(√12)^2=12+12=24;

CD=√24=2√6.

Периметр P(ABCD)=AB+BC+СD+AD=4+3+2√6+5+√12=2√3+2√6+12.

Площадь S(ABCD)=BH*(AD+BC)/2=2√3(5+2√3+3)/2=8√3+6.

См. скриншот.