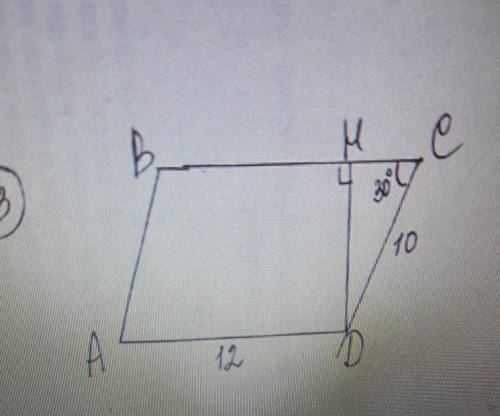
Дано :ABCD параллелограм , HD высота, угол DCH=30 ,CD 10 ,AD 12, угол DHB=90 найти : площадь параллелограмма

Из вершины В параллелограмма ABCD проведем высоту ВН к стороне AD. Рассмотрим треугольник АВН: угол АНВ = 90 градусов (так как ВН - высота, перпендикуляр), АВ = 6 см (по условию) - гипотенуза (так как лежит против угла 90 градусов), угол ВАН = угол А = 30 градусов (по условию). Катет ВН лежит против угла равного 30 градусов, поэтому:

ВН = АВ/2 (свойство прямоугольного треугольника);

ВН = 6/2 = 3 (см).

Площадь параллелограмма находится по формуле:

S = a*h,

где а - сторона параллелограмма, h - высота, опущенная на сторону а.

S = AD*BH;

S = 10*3 = 30 (см квадратных).

ответ: S = 30 см квадратных.