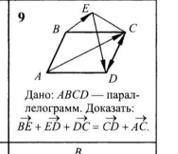
Дано: ABCD — парал-
лелограмм. Доказать:
BĚ + ED+DC = CD +Āč.

Чтобы доказать, что BĚ + ED+DC = CD +Āč, используем свойство параллелограмма, которое гласит: в параллелограмме противолежащие стороны равны и параллельны.

В данном случае, сторона AB параллельна стороне CD, поскольку обе они являются основаниями параллелограмма ABCD. Также сторона BE является диагональю параллелограмма ABCD.

Используем свойство параллелограмма:

BĚ + ED = CD (свойство в параллелограмме)
ED + DC = Āč (свойство в параллелограмме)

Сложим эти два уравнения:

BĚ + ED + ED + DC = CD + Āč

BĚ + 2ED + DC = CD + Āč

Учитывая, что 2ED эквивалентно ED + ED, заменим BĚ + 2ED на BĚ + ED:

BĚ + ED + DC = CD + Āč

Таким образом, мы доказали, что BĚ + ED + DC равно CD + Āč, используя свойства параллелограмма.