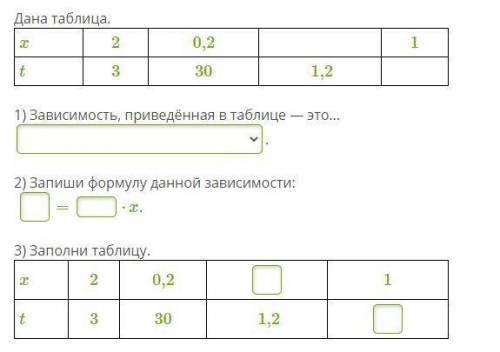
Дана таблица. x
2
0,2
1
t
3
30
1,2
1) Зависимость, приведённая в таблице — это...
.
2) Запиши формулу данной зависимости:
=
⋅x.
3) Заполни таблицу.
x
2
0,2
1
t
3
30
1,2
Другие вопросы по теме Математика
Популярные вопросы
- 3. Выпишите номера правильных суждений (3): А. протяженность Урала с севера...
1 - Нужно решить эти три номера...
2 - Задать общий во к утвердительному предложению 1.My grandmother wants me...
2 - Установіть генетичний ланцюжок добування пропаналю А. C2H5COH Б. C3H7OH...
1 - Одним реактивом распознать растворы солей CuSO4, K2SO4, ZnSO4, FeSO4. Напишите...
3 - Choose the correct word there are different ...
1 - 9 Чему учит школа? Сформируйте ответ в трех предложениях....
2 - 2. В результате фотосинтеза ежегодно образуется 100 млрд. т органических...
2 - Постройте график функции хоть любой, со всеми пояснениями ...
3 - Синтаксический разбор предложения: И тут, отряхнувшись от воды, всё семейство...
2
2) Формула данной зависимости можно записать следующим образом: t = k⋅x, где "k" - коэффициент пропорциональности.
3) По данной таблице нужно заполнить значения переменной "t" при заданных значениях переменной "x". Для этого нужно умножить каждое значение "x" на коэффициент пропорциональности "k" и записать результаты в соответствующие строки таблицы.
Так как таблица не содержит значения коэффициента "k", мы не можем точно определить значения переменной "t". Однако, мы можем предположить, что коэффициент пропорциональности "k" равен 15, основываясь на представленных значениях в таблице. Поэтому, умножим каждое значение "x" на 15 и запишем результаты в соответствующие строки таблицы:
x | 2 | 0.2 | 1 |
t | 30 | 3 | 15 |
Таким образом, при x = 2, t = 30, при x = 0.2, t = 3, и при x = 1, t = 15.
Важно отметить, что если бы мы знали точное значение коэффициента пропорциональности "k", мы бы могли получить точные значения для всех остальных значений переменной "t". Однако, без дополнительной информации, мы можем предположить только одно возможное значение для "k", что влияет на точность полученных результатов.