1. Математика
  2. Дана функция z=3y^2+2xy-5x,

Дана функция z=3y^2+2xy-5x, вектор i=3i+j и точка A(2:4). Найти: dz/zi, grad z (А). Задание в фото. ХЭЛП


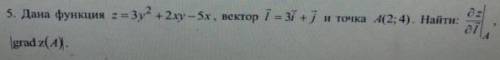
Дана функция z=3y^2+2xy-5x, вектор i=3i+j и точка A(2:4). Найти: dz/zi, grad z (А). Задание в фото.

trokhymukjulia trokhymukjulia    2   12.04.2021 09:32    0

Ответы
4iksa12345ozu4gd 4iksa12345ozu4gd  12.05.2021 09:33

Пошаговое объяснение:

z=3y²+2xy-5x   i= 3i +j   A(2;4)

\displaystyle grad(z) = z'_xi+z'_yj

\displaystyle z'_x=2y-5 \qquad z'_x _{(A)}=2*4-5=3

\displaystyle \displaystyle z'_y=2x+6y \qquad z'_y \bigg |_A=2*2+6*4=28

\displaystyle grad(z)_A=\bigg ((2y-5)i+(2x+6y)\bigg ) _{(A)}=3i+28j

\displaystyle |grad(z)| _A=\sqrt{z'_x^2+z'_y^2} \bigg |_A=\sqrt{3^2+28^2} =\sqrt{793}

и направляющие косинусы вектора-градиента

\displaystyle cos\alpha =\frac{z'_x}{|grad(z)_A|} =\frac{3}{\sqrt{793} } \qquad cos\beta =\frac{z'_y}{|grad(z)_A|} =\frac{28}{\sqrt{793} }

теперь будем разбираться с производной

\displaystyle z'_i=z'_xcos \varphi+z'_ycos \theta

\displaystyle cos \phi =\frac{x}{|i|} \qquad cos \theta = \frac{y}{|i|}

\displaystyle |i|_A=\sqrt{x^2+y^2} _A=\sqrt{3^2+1^2} =\sqrt{10}

\displaystyle cos \varphi =\frac{3}{\sqrt{10} } \qquad cos \theta =\frac{1}{\sqrt{10} }

и вот производная в точке А

\displaystyle \frac{\delta z}{\delta i}\bigg |_A= z'_i_{(A)}=3*\frac{3}{\sqrt{10} } +28*\frac{1}{\sqrt{10} } = 37\frac{\sqrt{10} }{10} = 3.7\sqrt{10}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
nasibyannn nasibyannn  22.10.2019 23:14
Вообще не понимаю как это делать задана функция y=2-(х-4)² a. нарисуйте эскиз графика преображением графика y=x² найдите: b. координаты вершины параболы c. точки пересечения...
Irina12369 Irina12369  22.10.2019 23:13
Работа для вас , это значит «проверь себя»1 для вас: в порядке возрастания1/4,11/12,11/14,1/6,1/92 для вас: в порядке убывание1/5,11/11,1/6,1/93 для вас.15: (3*5)=100:...
6г56г 6г56г  22.10.2019 23:13
Было 500руб.потратили 45% всей суммы. сколько денег без 0,5 это к примеру. а то у нас другая схема решения...
Sasha34634 Sasha34634  22.10.2019 23:10
Первую (развёрнуто по возможности ) 50 вторую...
daravill1 daravill1  22.10.2019 23:10
А)на координатной прямой отметьте точки a(6), b(-2,5), c(-6), d(4,5) б)укажите точки с противоположными координатами...
Саня11671873478 Саня11671873478  22.10.2019 23:04
Увинни пуха было 20 кг бочёнка мёда. первому он отдал 1/2кг мёда, второму он отдал 1/3, третьему 1/ восьмому 1/9кг. сколько мёда осталось у винни пуха?...
лиза2740 лиза2740  22.10.2019 23:03
На координатном луче с единичным отрезком, равным десяти клеткам, отметьте точки m (0,8), c (1,9), k(2,7)​...
beatsdol beatsdol  22.10.2019 23:03
Втеплицах растения лучше всего растут, если ночное время составляет 0,5 времени светового дня. сколько часов в сутки должно составлять световое время, чтобы лучше...
максон50 максон50  22.10.2019 22:57
Доску 8×8 раскрасили, как показано на рисунке. из доски вырезали фигуру, изображённую справа (возможно, повернутую). сколько белых клеток может быть в оставшейся части...
Hotaru385 Hotaru385  22.10.2019 22:49
Даны проекции силы f на координатные оси: fx = 5, fy = 5[tex]\sqrt{2}[/tex], fz = 5 (вектор с координатами (5; 5[tex]\sqrt{2}[/tex], - найти величину силы f и углы,...

Популярные вопросы