Дана функция ф(x, y, z)=f(x/z,y/z)*z^3 нужно найти первые производные по x, y, z. например: ф'x=(f'x (x/z)'+f'y(y/z)')z^3=f'x(1/z) как то так остальные по y и z не могу найти
Ответы
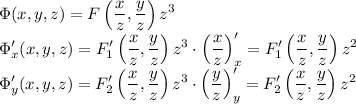
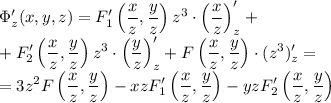
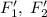 - производные функции F по первому и второму аргументу соответственно.
- производные функции F по первому и второму аргументу соответственно.
Другие вопросы по теме Математика
Популярные вопросы
- У50 великий і 25 менших банок розлили 200л виноградного соку. місткість...
2 - Одночасно з харкова і львіва вийшли два потяги,через 14 годин вони...
3 - Нужно завтра сдать, с решением 1)у=-5х если х=-0,3, то 2)у=-1/6х...
1 - Как изменится сила кулоновского взаимодействия двух зарядов,если...
1 - Впробирку с магнием добавить немного соляной кислоты. напишите...
2 - Написать сочинение на тему моя будущая професия тренер...
1 - Твір есе на тему моя улюблена акторка....
2 - Всовременной жизни фаткоры ( что делают )...
2 - Вкниге 3 повести. первая повесть занимает 50% всей книги, вторая...
3 - Подскажите песенки встречающиеся в сказках е шварца...
1