1. Математика
  2. Дана функция двух переменных.

Дана функция двух переменных. Найдите градиент в точке (-2;-4). ответ запишите в виде "(-19;52)" без пробелов и через точку с запятой.

jdkxnVAkx jdkxnVAkx    2   25.04.2022 20:33    0

Ответы
sertarsertar205 sertarsertar205  25.04.2022 20:40

\boxed{\boldsymbol{ \mathrm {grad}\ z = (-17; -7)}}

Пошаговое объяснение:

Функция: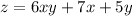 z = 6xy + 7x + 5y

Частные производные:

\dfrac{\partial z}{\partial x} = (6xy + 7x + 5y)_{x}' = 6y + 7

\dfrac{\partial z}{\partial y} = (6xy + 7x + 5y)_{y}' = 6x + 5

Градиент:

\mathrm {grad}\ z = \dfrac{\partial z}{\partial x}i + \dfrac{\partial z}{\partial y}j

Градиент функции z в точке (-2;-4):

\dfrac{\partial z}{\partial x} \bigg|_{ (-2;-4)} = 6 \cdot (-4) + 7= -24 + 7 = -17

\dfrac{\partial z}{\partial y} \bigg|_{ (-2;-4)} = 6 \cdot (-2) + 5= -12 + 5 = -7

\boldsymbol{ \mathrm {grad}\ z = -17i -7j}

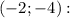
Градиент в координатной форме:

\boldsymbol{ \mathrm {grad}\ z = (-17; -7)}

ПОКАЗАТЬ ОТВЕТЫ
Klinyushina Klinyushina  25.04.2022 20:40

Пошаговое объяснение:

Задана функция:

f(x) = 6·x·y + 7·x + 5·y

Точка:

M (-2, -4)

Найдем частные производные:

f'(x) = 6x + 5

f'(y) = 6y + 7

Тогда:

f'(-2) = 6·(-2) + 5 = -12 + 5 = -7

f'(-4) = 6·(-4) + 7 = - 24 + 7 = - 17

Градиент в точке:

grad = -7·i - 17·j

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Aliya205 Aliya205  11.02.2022 19:19
1)-6,4+10,2= 2)-19,6-4,6= 3)-6,6-(12,3)= 4)-4,6+(-5,9)=...
heartanime heartanime  11.02.2022 19:20
Встановити відповідність між функцією та її областю визначення. Функція 1у=9/х2-4 2у= х-5 3у=10/х 4у=25/(х+5)(х-2) Область визначення Всі числа,1 крім 4 2Всі числа Всі числа,...
kristinazmataeva kristinazmataeva  11.02.2022 19:24
ответьте 3,14подилити на 48...
robka2029 robka2029  11.02.2022 19:25
Які речовини й у якій кількості утворяться в результаті взаємодії ета нової кислоти масою 3 г з ізоаміловим спиртом? Добудьте цю речовину з ви значеної в попередньому дослiдi...
dary090 dary090  11.02.2022 19:25
2.Какой из ответов правильный, если a||b, b|c, c|d? если А) а|d, b|d, Б) a|c, b||d, B) a||c, a|d, Г) а|c, a|d, b|d....
админ1273 админ1273  11.02.2022 19:26
Найди делимое если делитель равен 12 не полное частное 6 остаток 1...
hava27 hava27  11.02.2022 19:30
Знайдіть невідомі кути трекутника MNK,якщо MN=35см,MK=7см,/K=140міліметрів...
kebabchik111 kebabchik111  11.02.2022 19:32
Розташуйте числа в порядку зростання: 7,4; 3,15; 3,6; 5,060; 5,2; 7,28....
58684 58684  11.02.2022 19:32
В году спортивный магазин «Здоровье» приобрёл детских электросамокатов на сумму 390000 рублей по цене одного самоката 13000 рублей. На сколько меньше детских электросамокатов...
KatyaDro KatyaDro  11.02.2022 19:33
Выполните самостоятельно и пришлите на проверку: 1) 10x-2(3x-2) 52) 2x-5(2-3x) 73) 3x-4(2x-3)≤134) 10x-3(3x-2) 45) 4-8(x-2) 10-4x дам 50...

Популярные вопросы