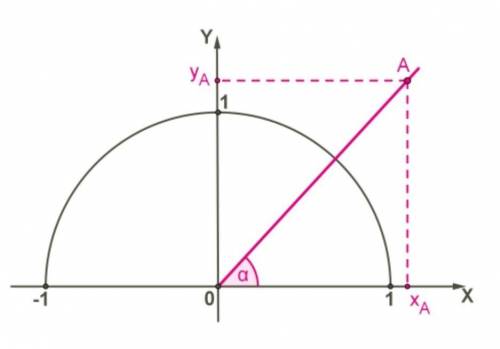
Дан угол α = 45°, который луч OA образует с положительной полуосью Ox, длина отрезка OA = 82.
Определи координаты точки A.

ответ: A ( √; √)​

Для определения координат точки A, мы можем использовать понятие тригонометрических функций.

Дано, что угол α = 45°, а луч OA образует с положительной полуосью Ox. Также известно, что длина отрезка OA = 82.

Поскольку угол α равен 45°, мы можем использовать значения тригонометрических функций для этого угла.

Определим значение синуса угла α. Синус угла α определяется как отношение противолежащего катета к гипотенузе прямоугольного треугольника.

В данном случае, противолежащий катет (вертикальная сторона треугольника) это координата y точки A, а гипотенуза (гипотенуза треугольника) это длина отрезка OA.

Таким образом, sin α = y / OA.

Подставим известные значения: sin 45° = y / 82.

Так как sin 45° равен √2 / 2, получаем следующее уравнение: √2 / 2 = y / 82.

Решим уравнение относительно y:

y = (√2 / 2) * 82.

Упростим выражение: y = 41√2.

Теперь определим значение косинуса угла α. Косинус угла α определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника.

В данном случае, прилежащий катет (горизонтальная сторона треугольника) это координата x точки A, а гипотенуза (гипотенуза треугольника) это длина отрезка OA.

Таким образом, cos α = x / OA.

Подставим известные значения: cos 45° = x / 82.

Так как cos 45° равен √2 / 2, получаем следующее уравнение: √2 / 2 = x / 82.

Решим уравнение относительно x:

x = (√2 / 2) * 82.

Упростим выражение: x = 41√2.

Таким образом, координаты точки A равны (41√2; 41√2).