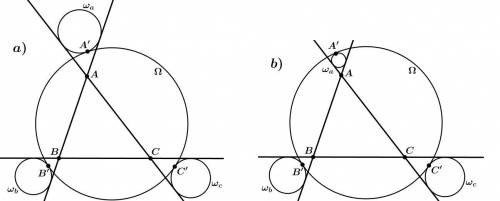
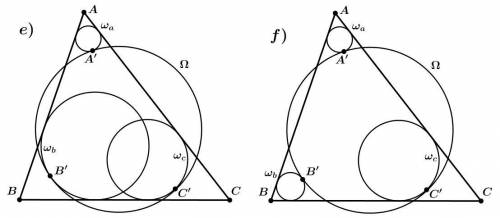
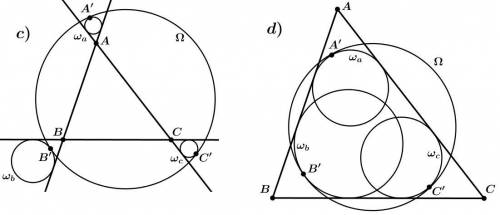
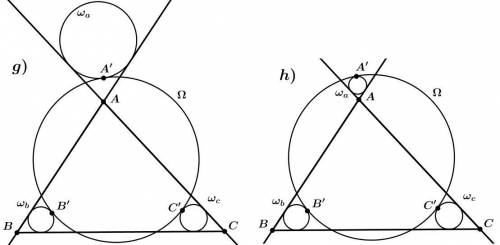
Дан треугольник ABC и окружность Ω. Окружность ωa касается прямых AB и AC, а также окружности Ω в точке A′. Аналогично определяются точки B′ и C′. В каких из приведенных ситуаций можно утверждать, что прямые AA′, BB′, CC′ пересекаются в одной точке?

Для решения этой задачи нужно рассмотреть каждую из предложенных ситуаций и определить, в каких случаях прямые AA', BB', CC' пересекаются в одной точке.

1. В первой ситуации окружность ωa касается прямых AB и AC, а также окружности Ω в точке A'. Заметим, что прямая, которая соединяет центр окружности ωa с точкой A', является высотой треугольника ABC. Так как каждый треугольник имеет три высоты, то треугольник ABC имеет три высоты AA', BB' и CC'. Если окружность ωa касается прямых AB и AC, то прямые AA', BB' и CC' будут пересекаться в одной точке, которая называется ортоцентром треугольника.

2. Во второй ситуации окружность ωb касается прямых AB и BC, а также окружности Ω в точке B'. Аналогично предыдущему случаю, заметим, что прямая, которая соединяет центр окружности ωb с точкой B', является высотой треугольника ABC. Так как окружность ωb касается прямых AB и BC, то прямые AA', BB' и CC' также будут пересекаться в одной точке, которая является ортоцентром треугольника.

3. В третьей ситуации окружность ωc касается прямых AC и BC, а также окружности Ω в точке C'. Аналогично предыдущим случаям, заметим, что прямая, которая соединяет центр окружности ωc с точкой C', является высотой треугольника ABC. Так как окружность ωc касается прямых AC и BC, то прямые AA', BB' и CC' также будут пересекаться в одной точке, которая является ортоцентром треугольника.

4. В четвертой ситуации ни одна из окружностей ωa, ωb и ωc не касается двух прямых одновременно. В данном случае прямые AA', BB' и CC' могут быть параллельными или совпадающими. Они все равно пересекаются бесконечно далеко от треугольника ABC, но не в одной точке.

Таким образом, можно утверждать, что прямые AA', BB' и CC' пересекаются в одной точке только в первых трех ситуациях, где соответствующие окружности касаются двух прямых и окружности Ω. В четвертой ситуации, прямые AA', BB' и CC' не пересекаются в одной точке.