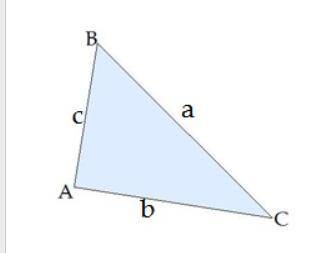
Дан треугольник ABC.
AC= 17,4 см;
∢ B= 45°;
∢ C= 60°.
ответ: AB=
Другие вопросы по теме Математика
Популярные вопросы
- Выберите страны, занимающие прибрежное положение: бразилия; австрия; монголия;...
2 - А)-3х=-21 б)-2/5х=3/10 в)0,5х+0,15=0 г)0,3p-5=6-0,7p...
3 - Скласти невеликий вірш про тараса шевченка 20...
3 - Длина окружности 62,8см, найти радиос окружности...
1 - Выделить в предложении главные и второстепенные члены: я ложусь спать в...
2 - 40 . нужно вставить пропущенные слова as…as’ (‘so…as’), ‘than’, ‘of’. 1)tom...
3 - 35/6*12 3целых 5/6пятьшестых умножить на 12...
3 - Определите число молекул, содержащихся в 17г фосфина (ph3)...
2 - Изменить по падежам (с верхней полки)...
3 - Для ремонта коридора и комнаты купили 25 рулонов обоев.сколько рулонов пойдёт...
1
Теорема синусов гласит:
В треугольнике со сторонами a, b и c и противолежащими им углами A, B и C соответственно, отношение стороны к синусу противолежащего угла равно для каждой стороны:
a/sinA = b/sinB = c/sinC
В данном случае, мы можем использовать эту формулу для отношения сторон AB, BC и AC:
AB/sin∠C = BC/sin∠A = AC/sin∠B
Мы знаем сторону AC, поэтому мы можем подставить значения в эту формулу:
AB/sin60° = BC/sin45° = 17,4/ sin(180° - 45° - 60°)
AB/sin60° = BC/sin45° = 17,4/ sin75°
Давайте сначала найдем значение sin75°, чтобы продолжить с решением:
sin(180° - 45° - 60°) = sin(180° - 105°) = sin75°
Так как sin(180° - α) = sin α, мы можем просто написать sin75°.
Мы можем найти sin75°, используя тригонометрическую формулу:
sin(a + b) = sin a cos b + cos a sin b
sin(45° + 30°) = sin45° cos30° + cos45° sin30°
sin75° = (sqrt(2)/2) * (sqrt(3)/2) + (sqrt(2)/2) * 1/2
sin75° = (sqrt(6) + sqrt(2))/4
Теперь, когда у нас есть значение sin75°, мы можем найти BC, используя теорему синусов:
BC = AB * (sin45° / sin60°)
BC = AB * (1 /√3)
BC = AB/√3
Теперь мы можем записать теорему синусов для сторон AB и BC:
AB/sin60° = BC/sin45°
AB/(√3/2) = AB/ (1/√3)
2AB = AB * √3
AB = [AB * (√3)] / 2
Теперь мы знаем, что AB равно [AB * (√3)] / 2. Мы также знаем, что BC = AB/√3. Из этих двух равенств, мы можем заменить AB в выражении для BC:
BC = ([AB * (√3)] / 2) / √3
BC = AB * (√3 / 2) / √3
BC = AB / 2
Теперь у нас есть выражение для BC. Мы также знаем, что AB = BC * √3. Из этих двух равенств, мы можем заменить BC в выражении для AB:
AB = (BC * √3) * √3
AB = BC * (√3 * √3)
AB = BC * 3
Таким образом, мы получаем следующие два равенства:
AB = [AB * (√3)] / 2
AB = BC * 3
Из этих равенств, мы можем сформулировать уравнение, чтобы решить относительно AB. Умножим первое уравнение на 2:
2AB = [AB * (√3)]
2AB = AB * (√3)
AB = AB * (√3) * 2/√3
AB = AB * (2√3)/√3
AB = AB * 2
Теперь мы можем поделить оба равенства на AB:
1 = 2
Это уравнение не имеет решения. Возможно, в процессе решения возникла ошибка. Пожалуйста, проверьте данные и вопрос еще раз.