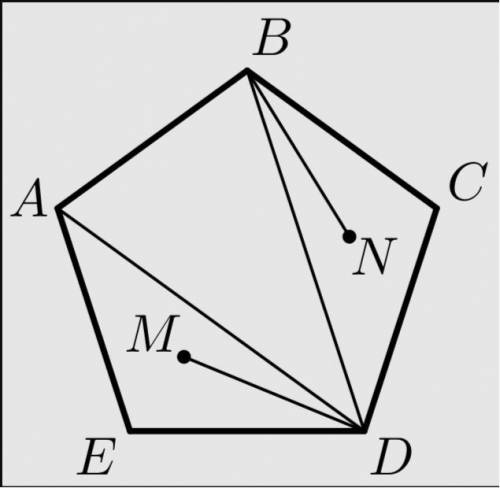
Дан правильный пятиугольник ABCDE, M и N — точки пересечения медиан треугольников ADE и BCD соответственно. Найдите угол между прямыми BN и DM. Углом между прямыми называется меньший из образованных ими углов.

Добрый день!

Чтобы решить данную задачу, давайте разберемся с основными понятиями и свойствами, которые нам понадобятся.

1. Правильный пятиугольник - это пятиугольник, у которого все стороны и углы равны между собой.

2. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Теперь перейдем к решению задачи.

У нас дан правильный пятиугольник ABCDE и точки M и N - точки пересечения медиан треугольников ADE и BCD соответственно.

Для начала, нам будет полезно знать некоторые свойства медиан треугольника:

1. Медианы треугольника пересекаются в одной точке, называемой центром тяжести треугольника. В нашей задаче точка пересечения медиан обозначена буквой G, но нам она не понадобится.

2. Медиана треугольника делит сторону треугольника в отношении 2:1. То есть, если мы возьмем отрезок AG и поделим его на две равные части, то получим отрезок GM, и отрезок GM будет в два раза короче, чем отрезок AG.

Теперь рассмотрим угол между прямыми BN и DM. Для этого построим вспомогательную прямую EG, которая будет являться медианой треугольника BCD. Заметим, что треугольники ADE и BCD подобны, так как у них равны углы при вершине E и B. Следовательно, прямые BN и DM также подобны.

Давайте посмотрим на отношение геометрических размеров медиан треугольников ADE и BCD. По свойствам медиан, отрезок DM будет в два раза короче отрезка MG, а отрезок BN будет в два раза короче отрезка NG. Отсюда следует, что отрезок BN в два раза короче отрезка DM.

Теперь давайте рассмотрим угол между прямыми BN и DM. Поскольку отрезок BN короче отрезка DM в два раза, то угол между прямыми BN и DM будет в два раза меньше, чем угол, образованный отрезком DN и вертикальной осью.

У нас есть прямоугольный треугольник DNK, где DK является вертикальной осью, а DN - это отрезок, рассматриваемый нами. Для нахождения угла между прямыми BN и DM, нам нужно найти угол KDN. Воспользуемся тригонометрией.

Мы можем использовать тангенс угла KDN для нахождения этого угла. Тангенс угла KDN можно найти как отношение противолежащего катета (DN) к прилежащему катету (DK):

tg(KDN) = DN / DK.

Отсюда, зная значения отрезков DN и DK, мы можем найти значение тангенса и, соответственно, сам угол KDN.

Если дан правильный пятиугольник ABCDE, у нас, к сожалению, отсутствуют конкретные численные значения для отрезков DN и DK, поэтому невозможно найти точное численное значение угла KDN.

Однако, мы можем сделать вывод о том, что угол между прямыми BN и DM будет меньше угла KDN, так как отрезок BN короче отрезка DM в два раза. То есть, угол между прямыми BN и DM будет меньше половины угла KDN.

Вот так можно решить данную задачу.