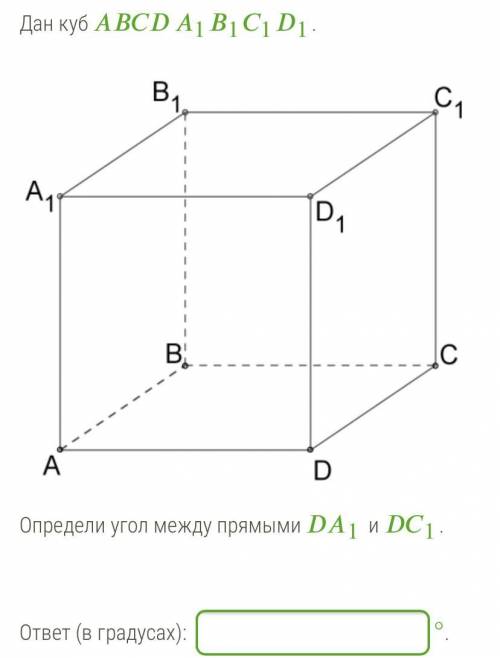
Дан куб ABCD A1B1C1D1.

Определи угол между прямыми DA1 и DC1.

Для определения угла между прямыми DA1 и DC1 в кубе, мы можем использовать знания о геометрии и свойствах куба.

Шаг 1: Понимание куба
Прежде чем перейти к решению вопроса, давайте разберемся с тем, что такое куб. Куб - это трехмерный геометрический объект, у которого все шесть граней являются квадратами. В кубе все ребра равны между собой, и все углы между ребрами равны 90 градусам.

Шаг 2: Изучение куба ABCD A1B1C1D1
В данном случае у нас есть куб ABCD A1B1C1D1. Визуализируя его, мы можем видеть, что прямые DA1 и DC1 являются диагоналями двух граней куба. Мы хотим определить угол между этими двумя диагоналями.

Шаг 3: Поиск свойств куба
Чтобы решить эту задачу, нам необходимо использовать свойства куба. Одно из свойств куба состоит в том, что диагонали плоскостей куба пересекаются в точке пересечения, которая лежит в середине общего ребра двух плоскостей. Таким образом, точка пересечения диагоналей DA1 и DC1 будет лежать на общем ребре плоскостей.

Шаг 4: Поиск ребра для построения равнобедренного треугольника
Теперь, зная свойства куба, мы можем найти общее ребро для прямых DA1 и DC1. Это будет ребро AD, так как оно образует общую грань для плоскостей, содержащих DA1 и DC1.

Шаг 5: Построение равнобедренного треугольника
Пусть точка M будет серединой ребра AD. Продолжим ребро DC до точки P, которая будет совпадать с точкой M. Теперь у нас есть треугольник DCP, и он является равнобедренным, так как ребра DP и CP равны друг другу (так как они образуют куб).

Шаг 6: Определение угла между прямыми DA1 и DC1
Теперь мы можем определить угол между прямыми DA1 и DC1, используя свойство равнобедренного треугольника. Угол A1DM будет равен углу MDC, так как эти два угла являются соответственно углами при основании равнобедренного треугольника.

Шаг 7: Вывод ответа
Таким образом, угол между прямыми DA1 и DC1 равен углу A1DM или MDC.

На этом месте я бы задумался оставить разобрать только эти шаги и дождаться интереса в решении, или оправшивал бы о знание угла закона синусов или косинусов, и задал бы задачу не о кубе, а о произвольном параллелепипеде или дополнительную метрику угловых сторон размерности на плоскости бумаги.