Дам 35 1

Пусть f(n) – количество натуральных чисел, взаимно простых с n и не превосходящих n. Для скольких чисел первой тысячи выполняется равенство f(9n)=9⋅f(n)?

2

На сторонах AB и BC треугольника ABC взяты точки K и M так, что AK:KB=k:1 и BM:MC=2:3. Отрезки AM и CK пересекаются в точке P. При каком наименьшем целом k отношение площади треугольника AKP к площади треугольника CMP также будет целым?

3

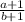Сколько существует пар натуральных чисел a и b, не превосходящих 500, таких, что числа и являются соседними натуральными числами (отличаются на 1)?

4

Найдите объём треугольной пирамиды ABCS, у которой SA=12, BC=4, а остальные рёбра равны 7.

5

Для целых чисел x и y выполняется равенство 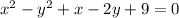. Какое наибольшее значение может принимать модуль разности квадратов x и y?

6

Натуральное число n назовём (a,b)-представимым, если его можно представить в виде суммы нескольких слагаемых, равных либо натуральному числу a, либо натуральному числу b, но при этом число n+1 так представить нельзя. Найдите наибольшее (1001,2022)-представимое число.

gurboolga    1   06.11.2021 03:48    6