D(M,AD)=d,(M,BC)=d(M,AC)=5, AC=9,BC=12,M∉ABC
Найдите: d(M,ABC).
За решение
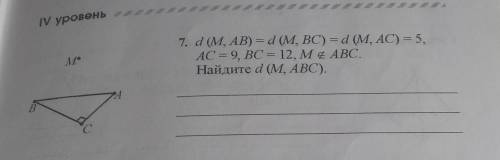
Другие вопросы по теме Математика
Популярные вопросы
- 4^x туюнтмасы кайсы мааниде 1ден чон а)x 0б)x 0в)x 1г)x 1 решать...
3 - График уравнения 4х+2у-2 пересекает ОХ в точке:...
2 - 1. 2080 жылы өмір сүретініңізді елестетіп көріңіз. Виртуалды шындықты күнделікті...
3 - LUR you deA great Kyrgyz sportsman and writerEmir Sultankanov is one of the organizers...
3 - Роман Тургенева Отцы и Дети 1 отношение к аристократии Николая Петровича Кирсанова...
3 - Вычислить определитель пятого порядка...
2 - Нужно ответить на эти вопросы по каждому из 4х героев. 1. какими качествами характера...
2 - Кому не лень Вставьте И или Е. Подчеркните вставленную букву. Объясните свой выбор....
2 - Pu.882. Изобразите на координатной прямой точки A(1) B(8,3) C(-6) D(6) M(-2,4)...
3 - При ответах на комплимент используются определенные этикетные формулы. Укажите...
2
ответ: 4 .
ΔАВС , d(М,АВ)=d(М,ВС)=d(М,АС)=5 , АС=9 , ВС=12 , М∉АВС , ∠С=90°
Найти d(M,ABC) .
По теореме Пифагора: АВ=√(АС²+²ВС²)=√(9²+12²)=√225=15 .
MN⊥AC , MT⊥BC , MK⊥AB ⇒ d(М,АВ)=MK , d(М,ВС)=MT , d(М,АС)=MN .
MK=MT=MN=5 .
Так как расстояние от точки М до сторон треугольника одинаковое, то точка М проектируется на плоскость треугольника АВС в центр вписанной окружности О . d(M,ABC)=MO .
MO⊥ABC , ON=OT=OK= r (радиусу вписанной окружности) .
∠MON=∠MOT=∠MOK=90° , ΔMNO=ΔMTO=ΔMNO (по катету и гипотенузе)
По теореме Пифагора имеем: