Cos24° - cos84° sin54° решите подробно .
Ответы
Воспользуемся формулой: 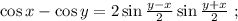
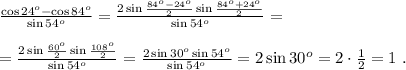
ПОКАЗАТЬ ОТВЕТЫ
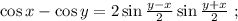
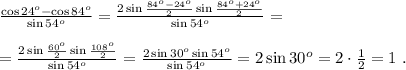
Другие вопросы по теме Математика
Популярные вопросы
- Из древней руси начала 12 века дошло до нас получение детям князя...
2 - (х+100)все в квадрате-2004(х+100)-2005=0...
2 - Двое рабочих изготовили 657 деталей,причем первый изготовил 63 деталей...
2 - Ж.б ламарк: какие были взгляды на эволюцию? причины эволюции? чарлз...
3 - Тело брошенное вертикально вверх со скоростью 9 м/с на какой высоте...
2 - Запишите данные слова методом письма водонепроницаемый - повышение...
3 - Какая масса 10%-раствора азотной кислоты должна быть введена во взаимодействие...
3 - Cвете втрое больше лет, чем было максиму тогда, когда она была в...
1 - Как доказать, что все вершины трапеции лежат в одной плоскости?...
1 - Мяч, который бросили с поверхности земли вертикально вверх, упал...
3