Чувачки , найти периметр трапеции если ab=cd=10, угол а=60 ad=16
Другие вопросы по теме Математика
Популярные вопросы
- кто всемирная история не могу понять вопросы...
2 - нужно составить текст рассуждение по упражнению 133 учебника по русской...
3 - Чем прославились в Отечественной войне 1812 года перечисленные военные?...
3 - Олимжона есть корзины и яблоки. Если положит в каждую корзину по 4 яблока,...
2 - Какие органы выводят продукты распада из организма 1) легкие2)печень...
3 - Каков объем деревянной плиты, если в воде на нее действует выталкивающая...
1 - Уменьшение объёма пузыря у рыб: * не влияет на плотность тела увеличивает...
1 - Власть безграничная природы нам потому не тяжела,что чувство видимой...
2 - Англ.Хэлппп Сопоставьте данные слова:awe,crouches,skilled,training,struggled,crawled,fierce,exhaustion,harsher,flew...
3 - 1. В системе координат нарисуй треугольник ABC с координатами вершин:...
3
Д. П.:
Проведем BH1 и BH2 - высоты.
1) AB = CD = 10, ⇒
ABCD - р./б. трапеция (по признаку р./б. трапеции), ⇒
∠A = ∠D = 60° (по св-ву р./б. трапеции)
2) Рассмотрим ΔABH1 (∠H1 = 90°)
∠ABH1 = 90° - ∠A = 90° - 60° = 30° (по т. о сумме углов в прямоуг. Δ),
⇒
AH1 =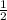 AB =
AB = 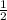 · 10 = 5 (по теореме)
· 10 = 5 (по теореме)
3) Рассмотрим ΔCDH2 (∠H2 = 90°)
∠DCH2 = 90° - ∠D = 90° - 60° = 30° (по т. о сумме углов в прямоуг. Δ),
⇒
DH2 =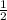 CD =
CD = 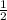 · 10 = 5 (по теореме)
· 10 = 5 (по теореме)
4) BC = H1H2 = AD - AH1 - AH2 = 16 - 5 - 5 = 6
5) P = AB + BC + CD + AD = 10 + 6 + 10 + 16 =42
ответ: P = 42