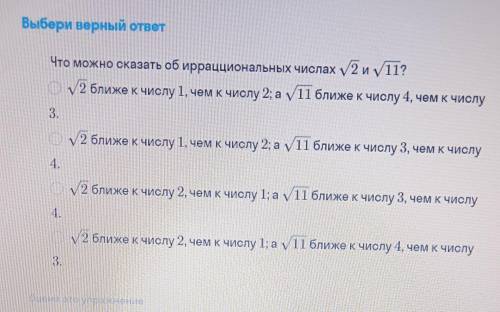
Что можно сказать об иррациональных числах √2 и √11?

Можно сказать, что иррациональные числа √2 и √11 являются числами, которые нельзя представить в виде дроби, то есть не могут быть записаны как отношение двух целых чисел.

1. Почему √2 является иррациональным числом?
Для доказательства иррациональности числа √2, воспользуемся методом от противного. Предположим, что √2 может быть записано в виде дроби p/q, где p и q - целые числа, и дробь p/q является несократимой (то есть числа p и q не имеют общих делителей, кроме 1).

Тогда мы можем возвести обе части уравнения (√2)^2 = (p/q)^2 в квадрат:
2 = (p^2) / (q^2)
2(q^2) = (p^2)

Из полученного уравнения видно, что число p^2 является четным числом, так как оно умножается на 2. Следовательно, number p также является четным числом (потому что квадрат нечетного числа всегда будет нечетным), и мы можем представить p в виде p = 2k, где k - целое число.

Подставляем значение p = 2k обратно в исходное уравнение:
2(q^2) = (p^2)
2(q^2) = (2k)^2
2(q^2) = 4k^2
q^2 = 2k^2

Из этого уравнения видно, что число q^2 также является четным числом. Следовательно, number q также является четным числом.

Противоречие: Мы предположили, что дробь p/q является несократимой, но у нас получилось, что оба числа p и q являются четными. Это означает, что наше предположение неверно и √2 не может быть представлено в виде рационального числа. Таким образом, √2 является иррациональным числом.

2. Почему √11 является иррациональным числом?
Доказательство иррациональности числа √11 можно провести аналогичным образом.

Допустим, что √11 может быть представлено в виде дроби p/q, где p и q - целые числа, и дробь p/q является несократимой.

Возводим обе части уравнения (√11)^2 = (p/q)^2 в квадрат:
11 = (p^2) / (q^2)
11(q^2) = (p^2)

Из уравнения видно, что число p^2 является нечетным числом, так как произведение числа 11 и q^2 является нечетным. Следовательно, число p также является нечетным числом (потому что квадрат четного числа всегда будет четным), и мы можем представить p в виде p = 2k+1, где k - целое число.

Подставляем значение p = 2k+1 обратно в исходное уравнение:
11(q^2) = (p^2)
11(q^2) = (2k+1)^2
11(q^2) = 4k^2 + 4k + 1
(4k^2 + 4k) = 11(q^2) - 1

Правая сторона уравнения является четным числом, так как 11(q^2) - 1 будет нечетным. Следовательно, левая сторона уравнения также должна быть четной.

2k^2 + 2k является четным числом, так как это произведение числа 2 на нечетное число (2k).

Противоречие: Мы предположили, что дробь p/q является несократимой, но получилось, что оба числа (2k^2 + 2k) и 11(q^2) - 1 являются четными числами. Это означает, что наше предположение неверно и √11 не может быть представлено в виде рационального числа. Таким образом, √11 является иррациональным числом.

Итак, мы доказали, что числа √2 и √11 являются иррациональными, то есть их нельзя представить в виде дроби, и это объясняет их непрерывную и бесконечно неповторяющуюся десятичную часть.