Числа p и q подобраны так, что парабола y=qx−x2 пересекает гиперболу xy=p в трёх различных точках a,b и c, причём сумма квадратов сторон треугольника abc равна 378, а точка пересечения его медиан находится на расстоянии 3 от начала координат. найдите произведение pq. ответ дайте в виде действительного числа, округлив его при необходимости стандартным образом до сотых. целую и дробную части разделяйте точкой. если возможных различных значений произведения pq окажется несколько, в ответе укажите их сумму.
Популярные вопросы
- 2. Сполученными словосочетаниями составьтепредложения.1.2.—...
1 - РЕБЯТ Я ПОКА ПОШЁЛ СРАТЬ ПРОЙДИТЕ ТЕСТ...
1 - Вычеслите произведение -64+79;-3,75+0,785,2,6--1,94,-1,46-8,98,49+52...
2 - Кто хочет подружиться со мной?...
3 - Определи, к какой сфере общества относится конкретный пример. Татьяна купила...
3 - 4. Complete the phrasal verbs with the correct preposition. Lily, can you...
1 - Практическая работа 6 по химии...
1 - На тонкой веточке рябины сидит серенький воробей. Надо подписать часть...
3 - Охрана природы и окружающей среды 1) считается личным делом каждого человека...
2 - 1. Автором гелиоцентрической системы является A) Галилей B) Ньютон C) Птолемей...
3
pq = 54
Пошаговое объяснение:
Пусть точки пересечения имеют вид ,
,  и
и 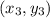 . Выразим через координаты то, что дано в условии.
. Выразим через координаты то, что дано в условии.
Сумма квадратов сторон:
(a - сумма квадратов, b - сумма попарных произведений)
Расстояние от начала координат до точки пересечения медиан
Известно, что координаты точки пересечения медиан можно найти по формулам:
Тогда квадрат расстояния от начала координат до точки пересечения медиан, для удобства умноженный на 9, выражается так:
Получилась система линейных уравнений на a и b. Из неё 4b = 2 * 81 - 378 = -216, b = -54. Осталось выразить сумму попарных произведений, для этого понадобится немного преобразовать систему и вспомнить теорему Виета.
Умножаем уравнение параболы на x и заменяем xy на p, получается кубическое уравнение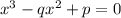 . Понятно, что найдя из этого уравнения x, потом по формуле y = p/x однозначно найдем y. Значит,
. Понятно, что найдя из этого уравнения x, потом по формуле y = p/x однозначно найдем y. Значит,  ,
, 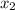 и
и 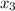 - корни кубического уравнения. По теореме Виета сумма их попарных произведений равна коэффициенту при x, он равен нулю.
- корни кубического уравнения. По теореме Виета сумма их попарных произведений равна коэффициенту при x, он равен нулю.
Умножаем уравнение параболы на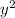 , избавляемся от x и получаем
, избавляемся от x и получаем  . Аналогично, нужна сумма попарных произведений, она равна -pq.
. Аналогично, нужна сумма попарных произведений, она равна -pq.
Приравниваем: