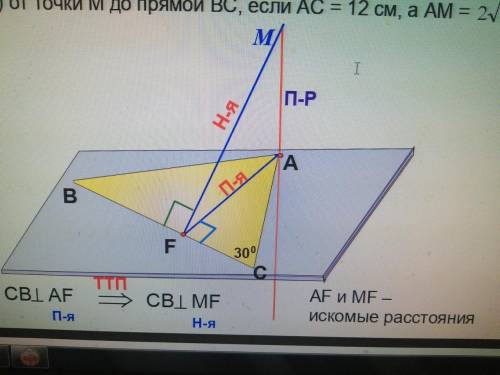
Через вершину С треугольника АВС проведена
прямая СМ, перпендикулярная к его плоскости. Угол С
равен 300. Найдите расстояния: 1) от точки А до прямой ВС;

2) от точки М до прямой ВС, если АС = 12 см, а АМ 2 корень из 3. см

П

Дано:

то по теореме о 3-х перпендикулярах МН ⊥ АВ.

ответ: 6 см

Для решения данной задачи, нам понадобятся знания о геометрии треугольников и тригонометрии.

1) Чтобы найти расстояние от точки А до прямой ВС, нам нужно определить высоту треугольника АВС, опущенную из вершины А на сторону ВС.

Для начала, обратимся к теореме синусов:
В треугольнике АВС, со сторонами АС = 12 см, ВС = ?, и угол С = 300, мы можем использовать соотношение:
sin(C) / ВС = sin(A) / АС

Заменяем известные значения:
sin(300) / ВС = sin(A) / 12

Переходим к обратному значению синуса:
ВС / sin(300) = 12 / sin(A)

Так как угол А равен 180 - 300 = 120, мы имеем:
ВС / sin(300) = 12 / sin(120)

Таким образом, мы можем найти значение ВС, используя тригонометрические функции и их обратные значения.

2) Чтобы найти расстояние от точки М до прямой ВС, нам нужно определить проекцию точки М на данную прямую.

Воспользуемся определением косинуса угла:
cos(C) = МС / АС

Заменяем известные значения:
cos(300) = МС / 12

Таким образом, мы можем найти значение МС, используя косинус угла С.

Теперь, когда у нас есть значения ВС и МС, мы можем использовать теорему Пифагора, чтобы найти расстояние.

Для 1):
Используем теорему Пифагора в треугольнике АВС:
ВС^2 = АС^2 + АВ^2

Подставляем известные значения:
ВС^2 = 12^2 + АВ^2

Таким образом, мы можем найти значение ВС.

Для 2):
Так как МС - это проекция точки М на прямую ВС, мы можем использовать треугольник МСВ, чтобы применить теорему Пифагора:
МС^2 = ВС^2 - МВ^2

Подставляем известные значения и найденное значение ВС:
(МС^2) = (ВС^2) - (МВ^2)

Таким образом, мы можем найти значение МС.

Для полного решения данной задачи, необходимо вычислить расстояния, используя соответствующие формулы и заменяя известные и найденные значения.