Чему равна сумма целых решений неравенства sinx(cos2x-1)>0 на промежутке [-пи; пи]
Другие вопросы по теме Математика
Популярные вопросы
- Як називають найбільші конвекційні потоки, що виниквють в атмосфері?...
1 - 8y+(y-6y)-(7-4y) упростить...
3 - Бетонную плиту объёмом 0,25 м3 равномерно подняли на высоту 6 м. Чему...
3 - Розв яжіть рівняння 1)х²+8х-20=02)4-9х²=03)х²-8х=0...
1 - Правда ли, что римские города не были благоустроены?...
2 - Дана правильная четырехугольная пирамида со стороной основания 4 и...
3 - 1 2. Найкращі, найродючіші грунти — чорноземи поширені у: а) помірних...
1 - отрезокКН-бессиктриса треугольника КДР.через точку Н проведена прямая...
3 - Что можно получить из морских водорослей в промышленных условиях чень...
2 - Скласти твір-опис природи за прочитаними творами (об єм 1сторінка.рукописного...
3
Пошаговое объяснение:
Так как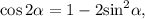 неравенство можно переписать так:
неравенство можно переписать так:
Учитывая заданный промежуток![[ - \pi ;\,\,\pi ],](/tpl/images/4978/5434/dfb70.png) следует найти сумму целых решений неравенства на промежутке
следует найти сумму целых решений неравенства на промежутке 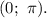
Так как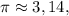 целыми числами, попадающими в такой промежуток, являются 1, 2 и 3. Их сумма равна 6.
целыми числами, попадающими в такой промежуток, являются 1, 2 и 3. Их сумма равна 6.