Бригада рабочих устанавливает столбы освещения на шоссе. им надо установить ровно 321 столб на одной стороне шоссе. каждый следующий день им надо устанавливать по одному столбу в промежутки между уже установленными столбами. на какое наибольшее число дней бригада сможет растянуть выполнение этого ? а) 4; б) 5; в) 6; г) 7; д) 8.
Другие вопросы по теме Математика
Популярные вопросы
- Размеры железнодорожной шпалы длина 2.5 м ширина 40 см и толщина 25 см чему равен...
3 - На числовом луче найдите координаты точек b и c,если известно,координата точки...
1 - Все объекты северной америки (равнины, горы, реки, озера и т.д)...
1 - Смысл пословицы труд человека кормит , а лень портит...
3 - Составь верные равенства в которых число 40 является а) множителем б) делимым...
3 - Переведите на язык ,употребляя глагол to be в present simple: 1)чей это брат?...
2 - Напсать проверочное слово хлопотать, ввечерело...
1 - 64,10,49,13,36,9,25 х найдите х и закономерность...
1 - Мне решить этот пример за это сердечко ...
3 - Сделать 2, 3 контрольные вопросы...
1
Найдем сколько столбов установила бригада после i-ого дня.
Пусть после предыдущего (i-1) дня стоит ровно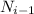 столбов.
столбов.
Т.к. каждый следующий день столбы устанавливаются строго между уже поставленными, то в i-ый день установят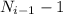 столбов.
столбов.
Тогда суммарно после i-го дня имеем:
(1)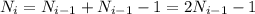
Теперь, выразим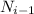 через
через 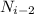 и подставим в выражение (1).
и подставим в выражение (1).
Продолжая выражать члены последовательности через предыдущие, через (i-1) шаг получим:
(2)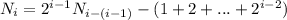 .
.
В этом выражении справа видим сумму (i-1) членов геометрической прогрессии c a1=1, q=2. Ее можно также представить в виде:
Подставим это в выражение (2):
(3)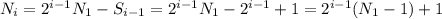 .
.
Перепишем получившееся выражение в более удобном виде:
(4)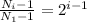 .
.
Теперь мы видим, что выражение, стоящее слева знака равенства должно быть степенью 2.
По условию в конце работы: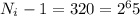
В таком случае, чтобы дробь была степенью 2, знаменатель должен быть вида:
(5)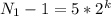 , где k =0,1,2...
, где k =0,1,2...
Для выполнения условия задачи, необходимо, чтобы в уравнении (4) i было максимально (чтобы работу можно было растянуть на максимальное кол-во дней). Значит нужно минимизировать знаменатель, а это значит выбрать минимальное k в выражении (5), т.е. k=0.
В таком случае: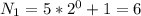
Подставим это в уравнение (4):
Отсюда заключаем, что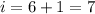 .
.
Таким образом, максимальное число дней в которые бригада сможет выполнить работу, сохраняя порядок работы, равно 7.