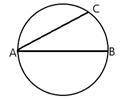
АВ – диаметр окружности, АС – хорда (см. рис.). Дуга АС больше дуги СВ. Градусные меры дуг АС и СВ относятся как 11 : 7. Найдите угол САВ.
Другие вопросы по теме Математика
Популярные вопросы
- Автомобиль двигаясь со скоростью 20 м/с путь 360 км, а затем за 3 часа...
2 - Каков объем воздушного шара, заполненного водородом, если масса газа 2,7...
3 - Фонетический разбор слова жалпыадамзатты...
1 - В каком веке сформировался жанр классической сонаты?...
2 - A) [121 - 185]эту просто вычислить надо...
2 - A.Navoiyning Saddi Iskandariy dostonidagi obrazlar tasnifi...
1 - Тебіндеп жайылатын малдың артықшылығын ата...
3 - Физика,4 вариант все задания...
3 - Два тела 0,6 и 150 кг находятся на расстоянии 3 км друг от друга.Определите,с...
1 - 9дм 4см-7дм5см= 5дм3см+3дм= 94см-75см= 2дм9см+27см= 53см+39см= Жаубтарын...
3
ответ: 35°
построй хорду СВ
угол АСВ, опирающийся на диаметр, равен 90°
т.к. это треугольник, сумма всех углов 180°
сумма двух оставшихся углов САВ и СВА равна 180°-90°=90°
из условия градусная мера дуги - это то же, что и угол, который образуется хордой и диаметром. другими словами градусная мера дуги АС - это то же что и угол СВА. градусная мера дуги СВ - это угол САВ (по рисунку ты это увидишь)
в итоге сумма градусных мер дуг СВ и АС = 90°, т.к. это то же, что и сумма углов САВ и СВА (смотри выше)
СВ+АВ = 90°
СВ+АВ=7+11 (из условия)
значит 90°=11+7=18
требуется найти угол САВ (или градусную меру дуги СВ - одно и то же)
составим пропорцию
90°=18
СВ=7
90°/18=СВ/7 (решаем уравнение)
90°*7=18*СВ
СВ= (90°*7) / 18 = 35° (ответ)
Для проверки можно найти градусную меру дуги АС (или угол АВС)
90°=18
АС=11
90°/18=АС/11
90°*11=18*АС
АС= (90°*11) / 18 = 55°
АС=55°
АС+ВС=55°+35°=90°, все сходится