Алексей вильнюсов наугад выбирает два натуральных числа p и q. найдите вероятность, что дробь p/q окажется несократимой.

Ответы

щувовтслалтв 11.10.2020 03:08

$\frac{6}{\pi^2}$

Пошаговое объяснение:

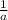Ясно, что дробь является сократимой, если у p и q есть общий простой делитель. Вероятность того, что произвольное число делится на простое число есть очевидно $\frac{1}{a}$ , а что не делится 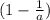$(1 - \frac{1}{a})$ . Также ясно, что делимость на разные простые числа - события независимые. Из вышесказанного следует, что вероятность того, что дробь не сокращается на простое число

$P=(1-\frac{1}{2^2})(1-\frac{1}{3^2})(1-\frac{1}{5^2})\dots$

Вспомним формулу суммы геометрической прогрессии:

$1+q+q^2+\dots=\frac{1}{1-q}=(1-q)^{-1}$

Отсюда

$1-q=(1+q+q^2+\dots)^{-1}$

Сделаем такое с каждой скобкой в нашем выражении для :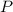

$P=(1+\frac{1}{2^2}+\frac{1}{2^4}+\dots)^{-1}(1+\frac{1}{3^2}+\frac{1}{3^4}+\dots)^{-1}(1+\frac{1}{5^2}+\frac{1}{5^4}+\dots)^{-1}\dots$

Тогда

$P^{-1}=(1+\frac{1}{2^2}+\frac{1}{2^4}+\dots)(1+\frac{1}{3^2}+\frac{1}{3^4}+\dots)(1+\frac{1}{5^2}+\frac{1}{5^4}+\dots)\dots$

Легко увидеть, что это равно

$P^{-1}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\dots$

т. е. сумме ряда обратных квадратов. Его значение можно легко получить например разложив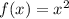 f(x)=x^2 в ряд Фурье и посмотрев значение в точке $x=\pi$ . Итак, сумма этого ряда есть