Ac=ab=17 см, bc=16 см. o - центр описанной окружности. ok перпендикулярно треугольнику abc, ok=5 см. ak - ?

Центр описанной около треугольника окружности находится в точке пересечения срединных перпендикуляров. 

Значит, для этого треугольника центр описанной окружности  лежит на его высоте АН, т.к. высота равнобедренного треугольника ещё и медиана, поэтому она - срединный перпендикуляр  к основанию ВС. . 

По т.Пифагора 

АН=√(AB²-BH²)=V(289-64)=15 см

Примем радиус описанной окружности равным R

По т.синусов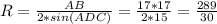

ОК  перпендикулярен плоскости ΔАВС. ⇒ ∆ АОК прямоугольный. 

По т.Пифагора 

АК=√(AO²+KO²)=√[(83521+22500):2]= ≈10,854 см