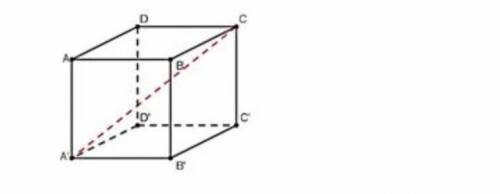
ABCDA'B'C'D 'Найдите косинус угла между плоскостью ABCD и прямой AC' в единичном кубе.

​

Для начала, чтобы решить эту задачу, нам нужно понять, что такое плоскость ABCD и прямая AC' в единичном кубе. Затем мы сможем найти косинус угла между ними. Единичный куб - это куб со стороной, равной 1. Плоскость ABCD образована точками A, B, C и D и состоит из всех точек, которые лежат на этой плоскости. Прямая AC' представляет собой прямую линию, проходящую через точку A и параллельную ребру C'D' единичного куба. Чтобы найти косинус угла между плоскостью ABCD и прямой AC', сначала нам нужно выразить их уравнения. Уравнение плоскости ABCD можно получить, используя векторное произведение двух векторов, направленных вдоль двух сторон плоскости. В нашем случае это можно сделать следующим образом: 1. Вычисляем векторы AB и AD, используя координаты точек A, B и D. AB = B - A = (1 - 0, 0 - 0, 0 - 0) = (1, 0, 0) AD = D - A = (0 - 0, 1 - 0, 0 - 0) = (0, 1, 0) 2. Вычисляем векторное произведение векторов AB и AD. AB × AD = ((0 * 0) - (1 * 1), (0 * 0) - (0 * 1), (1 * 0) - (0 * 0)) = (-1, 0, 0) Таким образом, уравнение плоскости ABCD имеет вид -x = 0 или x = 0. Замечаем, что x-координата равна нулю. Уравнение прямой AC' можно представить в параметрической форме, используя точку A и направляющий вектор C'D'. В одномерной форме это будет выглядеть следующим образом: AC' = A + t * C'D' где t - параметр, который принимает все возможные значения. Вектор C'D' можно найти, вычислив разность координат точек C' и D'. В нашем случае это будет: C'D' = D' - C' = (1 - 0, 1 - 0, 1 - 0) = (1, 1, 1) Теперь, используя выражение для AC' и значение вектора C'D', мы можем записать уравнение прямой AC': AC' = A + t * C'D' = (0, 0, 0) + t * (1, 1, 1) = (t, t, t) Таким образом, уравнение прямой AC' в параметрической форме будет x = t, y = t, z = t, где t принимает все возможные значения. Теперь мы можем найти косинус угла между этой прямой и плоскостью, используя их нормализованные вектора. Нормализованный вектор плоскости ABCD - это вектор, у которого длина равна 1. Мы уже знаем, что у этого вектора x-координата равна нулю, поэтому он имеет вид (0, y, z). Нормализованный вектор прямой AC' - это вектор, у которого длина также равна 1. Нам нужно найти этот вектор, но сначала найдем его длину. Длина вектора AC' равна корню из суммы квадратов его координат: |AC'| = sqrt(t^2 + t^2 + t^2) = sqrt(3t^2) = sqrt(3) * |t| Теперь мы можем найти нормализованный вектор прямой AC': AC' / |AC'| = (t, t, t) / (sqrt(3) * |t|) = (1/sqrt(3), 1/sqrt(3), 1/sqrt(3)) Таким образом, нормализованный вектор прямой AC' имеет вид (1/sqrt(3), 1/sqrt(3), 1/sqrt(3)). Наконец, нам нужно найти скалярное произведение нормализованных векторов плоскости ABCD и прямой AC', чтобы найти косинус угла между ними. Скалярное произведение векторов a и b определяется следующим образом: a · b = |a| * |b| * cos(θ), где θ - это угол между векторами. В нашем случае, скалярное произведение векторов плоскости ABCD и прямой AC' равно: (0, y, z) · (1/sqrt(3), 1/sqrt(3), 1/sqrt(3)) = 0 * 1/sqrt(3) + y * 1/sqrt(3) + z * 1/sqrt(3) = (y + z) / sqrt(3) Таким образом, косинус угла между плоскостью ABCD и прямой AC' в единичном кубе равен (y + z) / sqrt(3). Чтобы найти конкретное значение косинуса угла, нам необходимо знать значения y и z, которые определяются из уравнения прямой AC'. Но так как в данной задаче значения y и z не даны, мы не можем найти точное значение косинуса угла между плоскостью ABCD и прямой AC'.