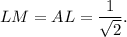ABC -прямоугольный треугольник. М э AC N принадлежит на продолжении стороны BC CM=BC, CN=AC BM перпендикулярна AN в точке L Найти LM
Другие вопросы по теме Математика
Популярные вопросы
- Маятник колеблется по закону х=0,4cos15,5t. период колебаний маятника равен...
3 - Что такое цена деления и как её находить? объясните !...
1 - Ссочинением. напишите сочинение на тему осенний ветер. попробуйте использовать...
2 - Доказать, что число ( m + 5п + 7)^6(3m + 7n + 2 )7 делится на 64 при любых...
1 - Дно её ровно и гладко. ровно и гладко-какая часть речи...
3 - Напишите небольшой рассказ за что я люблю свою собаку?...
2 - Подчеркни орфограмму безударные проверяемые гласные в корне слова тут прилетели...
1 - От какого слова образовано слово переводчик? !...
2 - Плохая шутка до добра не доведет.,какое предложение? повествовательное или...
1 - Найдите какое-нибудь число х, удовлетворяющее условию а≤ х ≤ b 1)a=0,83,...
3
Поскольку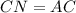 , то ΔACN — равнобедренный прямоугольный треугольник ⇒ ∠ANC = ∠NAC = 45°, значит прямоугольный треугольник ALM тоже равнобедренный ⇒
, то ΔACN — равнобедренный прямоугольный треугольник ⇒ ∠ANC = ∠NAC = 45°, значит прямоугольный треугольник ALM тоже равнобедренный ⇒ 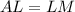 . Тогда
. Тогда 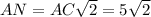 и
и 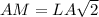 .
.
По теореме Менелая для треугольника
То есть,