А19.Найдите сумму всех целых решений неравенства:

Другие вопросы по теме Математика
Популярные вопросы
- Скільки буде 3 дициметри поділити на 6 ?...
3 - Самолёт вылетел из санкт-петербурга в читу в 10: 00 по московскому времени,расчётное...
3 - Проверочные слова к словам : наружность,вырастете...
2 - Вчём смысл и проблема данного высказывания: мы не хозяева собственной...
1 - Что такое ? ответье плэз за правильный ответ ставим...
1 - Спеременных m и t запишите переместительные свойства сложения и умножения....
3 - Они плавали по морям северного ледовитого океана...
3 - На завтра ! как проверить букву и в слове женщины,как проверить букву...
3 - 1что такое жилки 2 из каких частей состоит лист 3 каке виды вы знаете...
2 - Какие части листа обеспечивают выполнение этих функций: фотосинтез ,...
3
Пункт 5) -26 .
Пошаговое объяснение:
Раскроем знак модуля:
1)Если х>0 ⇒ |x|=х ⇒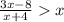
Так как числитель -x²-x-8<0 ,
а знаменатель x+4>0 ⇒
невыполнимо : ∅
2)Если x<0 ⇒ |x|=-x ⇒
3x-8+x²+4x=0
x²+7x-8=0
D=49-4·(-8)=81=9²>0
x₁=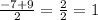
x₁=1>0 выпадает, так как положительно,
что противоречит выбранному условию.
x₂=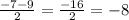
x₂=-8<0 подходит.
++++++++ _ _ _ _ _ _ _ _ _ _ _ ++++++++++++
--------------|-------------------------------|----------------------
_ _ _ _ _ -8_ _ _ _ _ +++++++1++++++++++++++
----------------------------|----------------------------------------
-4
x∈[-8; -4)∪[1: +∞)
Целые решения неравенства :
-8; -7; -6; -5.
Сумма всех целых решений
неравенства:
-8-7-6-5= -26 .