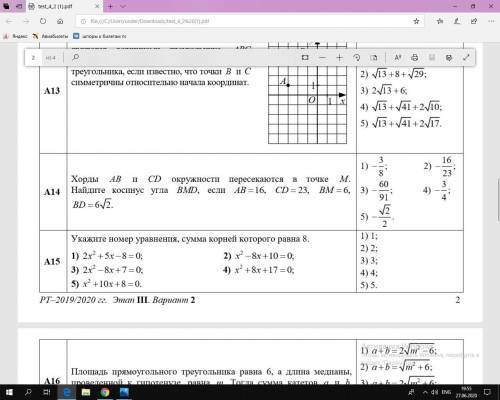
A14:Хорды AB и CD окружности пересекаются в точке . M Найдите косинус угла , BMD если AB=16,CD= 23, BM=6 ,BD= 6корней из 2
Другие вопросы по теме Математика
Популярные вопросы
- Черты сходства и различия природных зон евразии и северной америки по...
3 - Как изменится масса груза в 90 т, если его поднять на высоту 10 м? из...
3 - Скаким из перечисленных веществ кислород реагирует при обычных условиях?...
3 - Решение по . нужно решить часть b. нужны именно решения, а не просто...
1 - Как различить глюкозу и сахарозу - !...
1 - 1даны числа: 9; 30; 138; 6077; 10807. используя ms excel, вычисли среднее...
2 - Втреугольнике авс угол в прямой, ав=12см, вс=16см, к-середина стороны...
2 - Вариант 21. в таблице представлена смета расходов при покупке электротоваров.заполните...
1 - Запишите формулу объема прямоугольного параллелепипеда. вычислите неизвестную...
1 - Составьте по этой схеме предложения, умоляю, мне надо, умоляю просто...
2
Теорема косинусов гласит:
c^2 = a^2 + b^2 - 2ab*cos(C)
где a, b и c - стороны треугольника, C - противолежащий угол к стороне c, cos(C) - косинус угла C.
В треугольнике BMD известны следующие значения сторон:
BM = 6 и BD = 6√2.
Строим отрезок MD и обозначаем его длину как MD = x.
AB и BD - это хорды окружности, значит они равны радиусу окружности. Пусть радиус окружности равен r.
Таким образом, AB = BD = r.
Теперь мы можем записать уравнение теоремы косинусов для треугольника BMD:
MD^2 = BM^2 + BD^2 - 2BM * BD * cos(BMD)
Подставляем известные значения:
x^2 = 6^2 + (6√2)^2 - 2 * 6 * 6√2 * cos(BMD)
x^2 = 36 + 72 - 72√2 * cos(BMD)
Посмотрим на треугольник CMD и применим теорему Пифагора:
CD^2 = MD^2 + CM^2
Подставляем значения:
23^2 = x^2 + CM^2
529 = x^2 + CM^2
Мы уже знаем, что x^2 = 36 + 72 - 72√2 * cos(BMD).
Подставляем значение x^2:
529 = 36 + 72 - 72√2 * cos(BMD) + CM^2
Переносим значения на одну сторону уравнения:
529 - 36 - 72 = CM^2 - 72√2 * cos(BMD)
421 = CM^2 - 72√2 * cos(BMD)
Теперь мы должны найти значение cos(BMD). Для этого нужно перенести значения на другую сторону уравнения:
CM^2 = 421 + 72√2 * cos(BMD)
Из уравнения CD^2 = x^2 + CM^2:
529 = x^2 + 421 + 72√2 * cos(BMD)
Подставляем значение x^2:
529 = 36 + 72 - 72√2 * cos(BMD) + 421 + 72√2 * cos(BMD)
Подсчитываем значения:
529 = 529
Следовательно, это уравнение верно для любого значения cos(BMD).
Таким образом, косинус угла BMD может принимать любое значение в интервале от -∞ до +∞. Ответ: BMD не имеет определенного значения для данного треугольника.