9. Непрерывная случайная величина X распределена по нормальному закону с плотностью вероятностей f(x), где (картинка внизу) . Найти M[X], D[X]. Найти вероятность того, что в результате испытания X примет значение, заключенное в интервале (6;11).
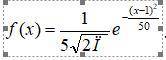
Другие вопросы по теме Математика
Популярные вопросы
- В каком году началась первая мировая война?...
3 - Расскажите об особенностях декоративной тематической композиции...
3 - Перевести на английский: Мой одноклассник готовит вкусный чай каждое...
3 - При сливании растворов гидроксида натрия и сульфата меди (2) выпал...
3 - Сочинения берегите в себе человека только не с интернета ...
2 - 1 We always ... each other. A Help. B helps. C helped 2. She never......
3 - В каком варианте ответа указаны предложения, в которых на месте пропуска...
3 - Два лесника собирали яблоки сколько они собрали если они утонули?...
1 - пристосування тварин до сумісного життя в природному угрупуванні/ при...
3 - ОТВЕТЬТЕ НА 2 ЗАДАНИЕ 362 1 • Спишіть текст, вставляючи пропущені літери...
3
Пошаговое объяснение:
Дан нормальный закон распределения:
В общем виде:
Математическое ожидание:
M[X] = a = 1
Среднее квадратическое отклонение:
σ = 5
Дисперсия:
D[X] = σ² = 25
Найдем:
P (α < X < β) = Ф ((β - a)/σ ) - Ф ((α - a)/σ)
По условию:
α = 6
β = 11
Тогда:
P (6 < X < 11) = Ф ((11 - 1)/5 ) - Ф ((6 - 1)/5)
P (6 < X < 11) = Ф (2) - Ф (1)
P (6 < X < 11) = 0,4772 - 0,3413 = 0,1359