8sin^2-2√3cos(π/2-x)-9=0. [-5π/2; -π]8sin^2-2√3sinx-9=08t^2-2√3t-9=0d=√300t1=2√3+10√3/16=(3√3/4)> 1 => пошел далеко и надолгоt2=2√3-10√3/16=(-√3/2)< 1 => многоуважаемыйsinx=-√3/2x=-π/3+2πnx=-2π/3+2πnподходит 1 корень - -7π/3все правильно?
Другие вопросы по теме Математика
Популярные вопросы
- решить 42 : 1 3/4- 15,6 + 1 2/3...
3 - У ТРИКУТНИКУ АВС: ВН - висота, Знайдіть довжину АН....
2 - Чему равно значение выражения 7 ab * (c + 5), если a = -1, b = 3, c = 5...
3 - 1. Из двух городов, между которыми равно 520 км, навстречу друг другу выехали...
2 - Доведіть що трикутник ABD = трикутнику COD якщо відомо що AB = CD і AB || CD КТО...
2 - Процессу глобализации : 1)Развитие отечественной культуры 2)Рост населения 3)Появление...
1 - За темою Образ майбутнього в літературі І рівеньВиберіть одну правильну відповідь1....
1 - 1) Магматические горы в основном залегают ... 1. На равнинах 2. В толщах осадочного...
1 - Для пакування подарунку взяли папір прямокутної форми. Його втявилось забагато,...
3 - У розповіді про сімейні негаразди в родині Буби використовується метафоричне порівняння...
3
а)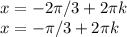 , где k∈Z
, где k∈Z
б) -7π/3
Пошаговое объяснение:
Произведём отбор корней.
Рассмотрим первую серию:
-5π/2 ≤ -2π/3+2πk ≤ -π
-11π/6 ≤ 2πk ≤ -π/3
-11/12 ≤ k ≤ -1/6
целых чисел k в этом диапазоне нет
Рассмотрим вторую серию:
-5π/2 ≤ -π/3+2πk ≤ -π
-13π/6 ≤ 2πk ≤ -2π/3
-13/12 ≤ k ≤ -1/3
Подходит целое число k=-1
x=-π/3-2π=-7π/3