1. Математика
  2. 80 номер Не могу решить неравенства

80 номер Не могу решить неравенства


80 номер Не могу решить неравенства

Soos2009 Soos2009    1   19.10.2020 02:27    0

Ответы
Nasti12 Nasti12  18.11.2020 02:28

1)

Найдем ОДЗ:

На 0 делить нельзя ⇒

x^2-64\neq 0\\x\neq \pm8

Упростим неравенство

\displaystyle \frac{x^2-7x-8}{x^2-64}

Разложим числитель и знаменатель на множители

\displaystyle \frac{(x+1)(x-8)}{(x-8)(x+8)}

Разберем все возможные случаи

\displaystyle \left \{ {{x+10}} \right. \\\\\left \{ {{x+10} \atop {x+8

Решаем

\displaystyle \left \{ {{x-8}} \right. \\\\\left \{ {{x-1} \atop {x

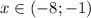
x \in (-8;-1)\\x \in \varnothing

ответ: x \in (-8; -1)

2)

Найдем ОДЗ:

На 0 делить нельзя ⇒

x^2-4\neq 0\\x\neq \pm2

Упростим неравенство

\displaystyle \frac{x^2+7x+10}{x^2-4} 0

Разложим числитель и знаменатель на множители

\displaystyle \frac{(x+2)(x+5)}{(x-2)(x+2)} 0\\\\\frac{x+5}{x-2} 0

Рассмотрим все возможные случаи

\displaystyle \left \{ {{x+50} \atop {x-20}} \right. \\\\\left \{ {{x+5

Решаем

\displaystyle \left \{ {{x-5} \atop {x+2}} \right. \\\\\left \{ {{x

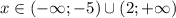
ответ: x \in (-\infty;-5)\cup(2;+\infty)

3)

Найдем ОДЗ:

На 0 делить нельзя ⇒

1-x^2\neq 0\\x\neq \pm1

Упростим неравенство

\displaystyle \frac{5x^2-3x-2}{1-x^2} \geq 0

Разложим числитель и знаменатель на множители

\displaystyle \frac{(5x+2)(x-1)}{(1-x)(1+x)} \geq 0\\\\\frac{-(5x+2)(1-x)}{(1-x)(1+x)} \geq 0\\\\\frac{-5x-2}{1+x} \geq 0

Решим систему неравенств

\displaystyle \left \{ {{-5x-2\geq0 } \atop {1+x0}} \right. \\\\\left \{ {{-5x-2\leq0 } \atop {1+x

\displaystyle \left \{ {{x\leq -\dfrac{2}{5} } \atop {x-1}} \right. \\\left \{ {{x\geq-\dfrac{2}{5} } \atop {x

ответ: x \in \bigg(-1; -\dfrac{2}{5} \bigg]

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
770glym 770glym  12.11.2020 18:19
найти какое число нужно вставить вместо вопросительного знака...
klarkwin klarkwin  12.11.2020 18:20
у книжці 120 сторінок Антон прочитав три чотири книжки а його однокласниця Оленка 2/5 хто прочитав більше сторінок І на скільки​...
nastiakosovic nastiakosovic  12.11.2020 18:20
График квадратного трехчлена с целочисленными коэффициентами a, b, c пересекает ось OX в точках Х1 и Х2, а ось OY в точке Y0. Найдите наибольшее значение угла x1y0x2, ответ дать в...
jvhhvcx jvhhvcx  12.11.2020 18:20
1)1,6+3 целых 1/4 2)2 целых 3/5+3,4...
tanyushalyubim tanyushalyubim  12.11.2020 18:20
Знайти ціле, якщо 6\7 становить 168​...
TOPTopTOP1vvv TOPTopTOP1vvv  12.11.2020 18:20
Карабас-Барабас решил обезопасить себя и свой театр от проникновения посторонних лиц. Для этого он попросил Дуремара заменить старый ключ от тайной комнаты, который хранился у черепахи...
Kseniacаt Kseniacаt  12.11.2020 18:20
Выбери тупые углы AHE FGE AIG DEG ACE...
sirzikova sirzikova  12.11.2020 18:20
решить системы линейных уравнений матричным методом: 1 система) 2x₁-x₃=1 x₁-4x₂+2x₃=-5 x₁+x₂+3x₃=6 2 система) 4x₁+x₂-x₃=7 2x₁+3x₂=7 x₁-x₂+5x₃=6...
masik01012015 masik01012015  12.11.2020 18:20
1901) Поезд из 10 вагонов мимо наблюдателя за 8 с. Чему равна ско- рость поезда, если длина вагона 16 м?2) Кондуктор пассажирского поезда заметил, что встречный товарный поезд мимо...
victoriareih victoriareih  12.11.2020 18:21
У Светы и Марины вместе 69 конфет. У Светы на 13 конфет меньше, чем у Марины. Сколько конфет у Марины?...

Популярные вопросы