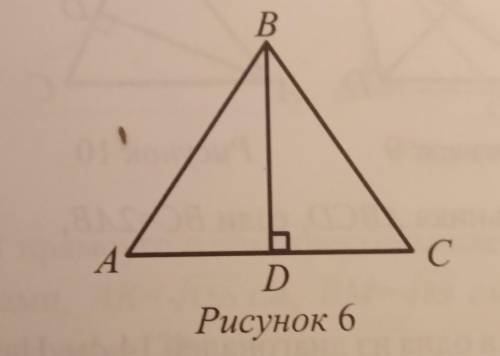
8. В треугольнике ABC с периметром 72 см, AB=BC, BDLAC, АС-АВ=12 см. Найдите BD (рисунок 6).

12 см

Пошаговое объяснение:

Т.к. треугольник равнобедренный,то возьмем его боковую сторону за x,тогда x+x+y=P,где P - периметр,получаем:

2х+y=72

Также АС-АВ=12 см по условию,значит y-x=12 ,составим систему и решим её:

          . Вычтем нижнее из верхнего,получим:

3х=60.Отсюда х = 20 см,т.е. АВ=ВС=20 см,а тогда АС= 20+12=32 см.

Рассмотрим треугольник CDB,у которого угол D равен 90 градусов.DC равно половине AC,т.к. высота в равнобедренном треугольнике также является медианой.По теореме Пифагора получим:

Отсюда BD=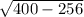 ==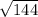12 см