(6n+1)²-1 делится или не делится на 12?

Да, делится.

Пояснение: чтобы доказать, что выражение делится на какое-либо число, нужно разложить его на множители и показать, что каждое из составляющих делится на это число.

В нашем случае сначала раскрываем первую скобку по формуле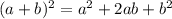 , затем единицы взаимно уничтожаются, после чего видим, что остаются два слагаемых, содержащих множитель 12.

Выносим его за скобки и делаем вывод, что да, выражение делится на 12.

Відповідь:

Покрокове пояснення:

(6 n-1)^2-1=36n^2-12n+1-1=36n^2-12n делится на 2,число четное