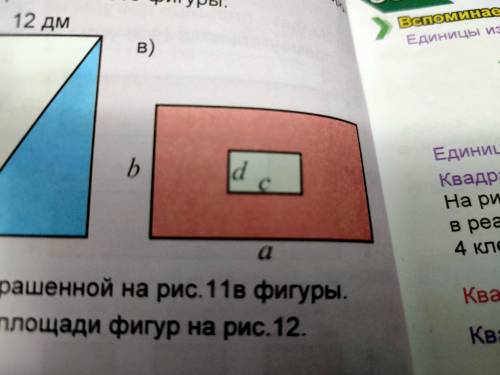
649. Найдите формулу для площади закрашенной на рис 11в фигуры.

Пошаговое объяснение:

(b*a) : (c*d)

Для нахождения формулы площади закрашенной на рис. 11в фигуры, нам необходимо разделить ее на две составные части: прямоугольник и треугольник.

Шаг 1: Найдем площадь прямоугольника.
Прямоугольник представлен на рисунке верхней частью закрашенной фигуры. Для нахождения его площади нужно умножить длину на ширину. По рисунку видно, что длина прямоугольника составляет 18 единиц, а ширина - 6 единиц. Поэтому площадь прямоугольника равна 18 * 6 = 108 квадратных единиц.

Шаг 2: Найдем площадь треугольника.
Треугольник заключенный в прямоугольнике представляет собой прямоугольный треугольник. Для нахождения его площади нужно умножить половину произведения катетов на гипотенузу. Катетами являются длина и ширина прямоугольника: 18 и 6 единиц соответственно. Гипотенузу можно найти с помощью теоремы Пифагора (a^2 + b^2 = c^2). Поэтому сначала найдем длину гипотенузы:

a^2 + b^2 = c^2
18^2 + 6^2 = c^2
324 + 36 = c^2
360 = c^2
c = √360
c ≈ 18.973 единиц

Площадь треугольника равна половине произведения катетов (18 * 6) и составляет:

площадь треугольника = (18 * 6) / 2 = 54 квадратных единиц.

Шаг 3: Посчитаем общую площадь закрашенной фигуры.
Для этого нужно сложить площадь прямоугольника и площадь треугольника:

площадь общей фигуры = площадь прямоугольника + площадь треугольника
площадь общей фигуры = 108 квадратных единиц + 54 квадратных единиц
площадь общей фигуры = 162 квадратных единиц.

Итак, формула для площади закрашенной на рис. 11в фигуры будет:

площадь = 162 квадратных единиц.