№6: в окружности проведены две пересекающиеся хорды ab=7, cd=5. точка их пересечения делит cd в отношении 2: 3. в каком отношении эта точка делит хорду ab? (в ответе укажите отношение меньшего отрезка к большему). выберите вариант ответа: 1: 7 5: 7 2: 3 1: 6 1: 5 № 7: диагональ трапеции делит её на два подобных между собой треугольника. отношение боковых сторон трапеции равно 2. найдите отношение большего основания трапеции к её меньшему основанию. выберите вариант ответа: 4: 2 4: 1 3: 1 3: 2 2: 1 № 4: решите систему уравнений {(2x+4)(y+5)=0,xy+y2=−1. выберите вариант ответа: (5,2; −5) (−2; 1) (−2; 1), (5,2; −5) (−1; 1), (5; −5) (1; −2), (−5; 5,2)

Ответы

AsakaKo 21.08.2020 19:23

18_03_09_Задание № 4:

Решите систему уравнений

$\left \{ {{(2x+4)(y+5)=0} \atop {xy+y^2=-1}} \right.$

РЕШЕНИЕ: Смотрим совокупность двух систем:

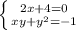
1) $\left \{ {{2x+4=0} \atop {xy+y^2=-1}} \right.$

Из первого уравнения найдем, что х=-2. Подставим во второе:

-2y+y^2=-1

y^2-2y+1=0

(y-1)^2=0

y=1

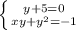
2) $\left \{ {{y+5=0} \atop {xy+y^2=-1}} \right.$

Из первого уравнения найдем, что х=-5. Подставим во второе:

-5x+25=-1

-5x=-26

x=5.2

ОТВЕТ: (-2; 1); (5.2; -5)

18_03_09_Задание № 6:

В окружности проведены две пересекающиеся хорды AB=7, CD=5. Точка их пересечения делит CD в отношении 2:3. В каком отношении эта точка делит хорду AB? (В ответе укажите отношение меньшего отрезка к большему).

РЕШЕНИЕ: Пусть О - точка пересечения хорд. Тогда, CO/DO=2/3=2x/3x.

Выразим CD: СD=CO+DO=2x+3x=5x=5, значит х=1. CO=2, DO=3

По теореме о пересекающихся хордах: АO*BO=CO*DO=2*3=6

С другой стороны АО+ВО=АВ=7. Выразим АО=7-ВО и подставим в теорему:

(7-ВО)*BO=6

BO^2-7BO+6=0

(BO-1)(BO-6)=0

ВО=1, тогда АО=6

или ВО=6, тогда АО=1

В любом случае отношение меньшей части к большей равно 1:6.

ОТВЕТ: 1:6

18_03_09_Задание № 7:

Диагональ трапеции делит её на два подобных между собой треугольника. Отношение боковых сторон трапеции равно 2. Найдите отношение большего основания трапеции к её меньшему основанию.

РЕШЕНИЕ: Пусть в трапеции ABCD такой диагональю является BD. Тогда накрест лежащие углы CBD и ADВ равны.

Так как в трапеции противолежащие углы не равны, то другие пары равных углов это ABD=BCD и BAD=BDC.

Отношение пропорциональных сторон: АВ/CD=AD/BD=BD/BC=2

Выразим из второй части: AD/BD=2, AD=2BD

Выразим из третьей части: BD/BC=2, BD=2BC

Подставляем: AD=2*2BC=4BC. Значит AD/BC=4.

ОТВЕТ: 4:1

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика