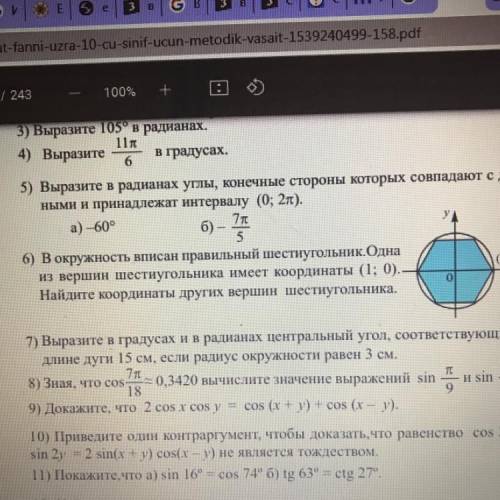
6) В окружность вписан правильный шестиугольник. Одна из вершин шестиугольника имеет координаты (1; 0)..
Найдите координаты других вершин шестиугольника.
надооо.
Другие вопросы по теме Математика
Популярные вопросы
- КотМатроскини заготовил 2/5 необходимого на зиму количества дров за 10 дней. Укажи,...
1 - 1. В какой форме должен играть футболист? а. Трико, гольфы, шиповки, наколенники....
1 - РЕШИТЕ ЭТУ ЗАДАЧУ В течение учебного года Иван несколько раз участвовал в соревнованиях...
1 - Английский 9 класс, проверочная работа на тему i wish...
2 - На плоское зеркало падает луч света. Определи, чему равен угол падения, если угол...
2 - Каждый образованный европеец должен иметь достаточное понятие о бессмертных созданиях...
2 - Тест для 5-7 классов (5 во В какой области 3D моделирование наиболее востребовано?...
3 - Материк наиболее и наименее гористой?...
1 - Найдите среднее арифметическое чисел 23,7; 29,4; 31,5;...
3 - Значение выражения a+8 в 7 раз меньше значения выражения 90-3a?...
3
Сначала построим окружность с центром в точке (0,0) и радиусом 1. Это делается с помощью уравнения окружности x^2 + y^2 = 1.
Так как шестиугольник правильный, его углы между соседними вершинами равны 120 градусам. Используя геометрические соображения, мы можем найти оставшиеся вершины шестиугольника.
Рассмотрим первую вершину шестиугольника с координатами (1,0). Угол между осью x и направлением от центра окружности к этой вершине равен 0 градусов. Теперь мы можем найти координаты других вершин, используя поворот вокруг центра окружности.
Повернем первую вершину на 120 градусов по часовой стрелке относительно центра окружности. Формула поворота точки (x,y) на угол a градусов относительно начала координат выглядит следующим образом:
x' = x*cos(a) - y*sin(a)
y' = x*sin(a) + y*cos(a)
Применяя эту формулу получаем:
x' = 1*cos(120) - 0*sin(120) = -0.5
y' = 1*sin(120) + 0*cos(120) = 0.866
Координаты второй вершины шестиугольника: (-0.5, 0.866).
Аналогично, повернем первую вершину на 240 градусов по часовой стрелке относительно центра окружности:
x'' = 1*cos(240) - 0*sin(240) = -0.5
y'' = 1*sin(240) + 0*cos(240) = -0.866
Координаты третьей вершины шестиугольника: (-0.5, -0.866).
Таким же образом, можно найти координаты остальных трех вершин шестиугольника:
- Четвертая вершина: (0.5, -0.866)
- Пятая вершина: (0.5, 0.866)
- Шестая вершина: (1, 0)
Таким образом, координаты других вершин шестиугольника:
(-0.5, 0.866)
(-0.5, -0.866)
(0.5, -0.866)
(0.5, 0.866)
(1, 0)