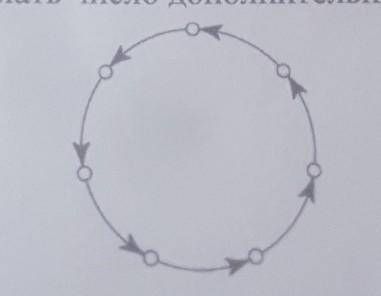
6.3 Семь городов соединены по кругу семью односторонними авиарейсами (см. рисунок). Назначьте (нарисуйте стрелочками, еще несколько односторонних рейсов так, чтобы от
любого города до любого другого можно было бы добраться, сделав не более двух
пересадок. Постарайтесь сделать число дополнительных рейсов как можно меньше.​УМОЛЯЮ

Чтобы решить эту задачу, нам нужно добавить несколько дополнительных авиарейсов, чтобы можно было добраться от любого города до любого другого с не более чем двумя пересадками.

В данной задаче есть семь городов, соединенных кругом. Для удобства назовем города A, B, C, D, E, F и G, в соответствии с изображением на рисунке.

1. Первым шагом мы можем добавить прямые рейсы из одного города в другой. Например, добавим рейс из города A в B, из B в C, из C в D и так далее, чтобы создать основу маршрута от одного города к другому.

2. Далее, нам нужно создать возможность пересадки в третьем городе. Для этого мы можем добавить рейс из города A в C, из B в D и так далее, чтобы создать путь, который позволяет добраться из одного города в другой с одной пересадкой. Теперь у нас есть рейсы A-B, B-C, C-D и так далее, а также рейсы A-C, B-D и так далее.

3. Наконец, нужно создать возможность для двойной пересадки. Для этого мы можем добавить прямой рейс от одного города к другому, чтобы создать путь с двумя пересадками. Например, мы добавим рейс из города A в D, из B в E, из C в F и из D в G. Теперь у нас есть рейсы A-B, B-C, C-D, D-E, E-F, F-G и так далее, а также рейсы A-C, B-D, C-E, D-F и G-A для создания маршрутов с двумя пересадками.

Таким образом, в результате наших добавлений мы получаем возможность добраться от любого города до любого другого с не более чем двумя пересадками.

Ниже представлено решение с добавленными рейсами:
A-B, B-C, C-D, D-E, E-F, F-G, G-A
A-C, B-D, C-E, D-F, G-A
A-D, B-E, C-F
A-E, B-F
A-F
A-G

В данном решении мы использовали минимальное количество дополнительных рейсов, чтобы обеспечить возможность добраться от любого города до любого другого с не более чем двумя пересадками.