1. Математика
  2. 5 вариант1. Найти угловой

5 вариант
1. Найти угловой коэффициент касательной к
графику функции в точке хо:
A) f(x)=x4 4х42х , хон-1
Б) f(x) sin x, xo п/2
В) f(x) у = 2ух , хог 2
2
| г) f(x)- 2 х , хент
?
Написать уравнение касательной в точке хо:
6x+x-10 x, x=-
A) f(x)=
2 x+1
х=-3
Б) f(x)=
Х
77
хо =
В) f(x)= tg x,​


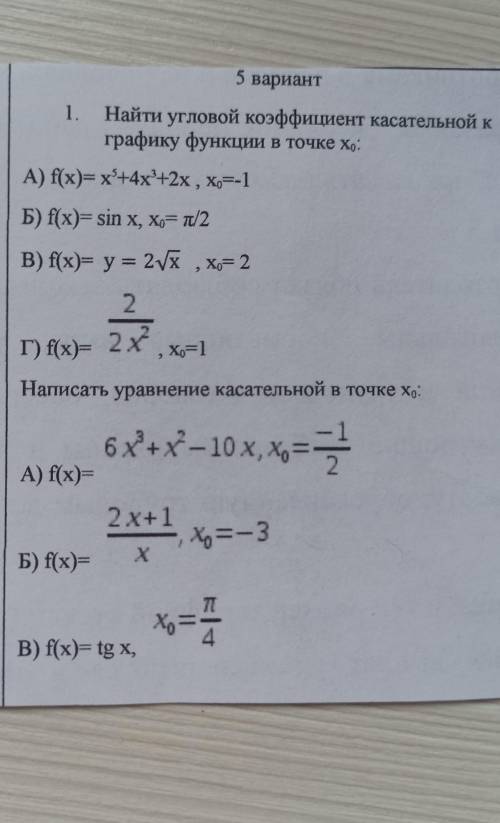
5 вариант1. Найти угловой коэффициент касательной кграфику функции в точке хо:A) f(x)=x4 4х42х , хон

простоя43 простоя43    2   11.04.2021 15:12    1

Ответы
vladimir1232 vladimir1232  11.05.2021 15:13

Пошаговое объяснение

1) f'(x) = 5x^4 + 12x^2 + 2\\f'(-1) = 5 + 1 + 2 = 8\\\\2) f'(x) = cosx\\f'(\pi/2) = cos(\pi/2) = 0\\\\3) f'(x) = \frac{2}{2\sqrt{x}} = \frac{1}{\sqrt{x}} \\f'(2) = \frac{\sqrt{2}}{2} \\\\4)f'(x) = \frac{-2}{x^3} \\f'(1) = -2\\\\1) f'(x) = 18x^2 + 2x - 10\\f'(-1/2) = -\frac{13}{2} \\f(-1/2) = \frac{9}{2}\\y = (x+\frac{1}{2} )*\frac{-13}{2} + \frac{9}{2}\\y = -\frac{13}{2}x + \frac{5}{4}\\\\

2) f(x) = 2 + \frac{1}{x} \\f(-3) = \frac{5}{3} \\f'(x) = -\frac{1}{x^2} \\f'(-3) = -\frac{1}{9} \\y = -\frac{1}{9}(x+3) + \frac{5}{3} \\y = -\frac{1}{9}x + \frac{4}{3} \\\\3) f'(x) = \frac{1}{cos^2x}\\f(\frac{\pi}{4}) = 1\\f'( \frac{\pi}{4}) = 2\\y = 2(x-\frac{\pi}{4}) + 1\\y = 2x - \frac{\pi}{2} + 1

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
зарема89 зарема89  07.04.2019 22:11
Кролик на 3 грядках посадил по 4 куста рассады. сколько всего капустной рассады посадил кролик. сделать схемотиче кий рисунок...
69Unicorn69 69Unicorn69  07.04.2019 22:10
Сколько процентов составляет число 67,9 от 350...
yyyye yyyye  07.04.2019 22:10
18 за решение: на координатной прямой отмечены точки а,в и с....
Биіккесамға Биіккесамға  07.04.2019 22:09
Туристы маршрута, и им осталось пройти 5км . какова длина всего пути? 6класс...
ryckovan3 ryckovan3  07.04.2019 22:07
Подготовьте сообщение. проценты были известны индусам ещё в v веке нашей эры. когда проценты появились в европе? что в этой связи опубликовал бельгийский учёный симон...
dkdjdhhs dkdjdhhs  07.04.2019 22:07
8\15-6\7= 13\6-9\8= 11\2-5\8= 7\34-2\17= 5\3-8\9= 11\80-4\15= 3\7-21\4=...
дашикмашикпык дашикмашикпык  07.04.2019 22:06
Тік бұрышты параллепипедтің ені 3см алдыңғы жағының биіктігі 2см және ауданы 12см оның баска жақтарының ауданын және көлемін есептеп тап ​...
BD20051 BD20051  07.04.2019 22:05
Вмагазине продавали 100 пирожных: картошка - 27 штук трубочки - на 3 штуки больше, остальные - корзиночки.сколько корзиночек продавалось в магазине ? ​решиь двумя...
Нияз2014 Нияз2014  07.04.2019 22:05
18 ! за решение: на координатной прямой отмечены точки а,в и с...
Айла2010 Айла2010  07.04.2019 22:04
18 ! за решение: на координатной прямой отмечены точки а,в и с...

Популярные вопросы