5!/(3!+4!) =
n!/((n-2)!) =
P_20/(P_4*P_16 ) =
A_25^2= ; C_36^5 =
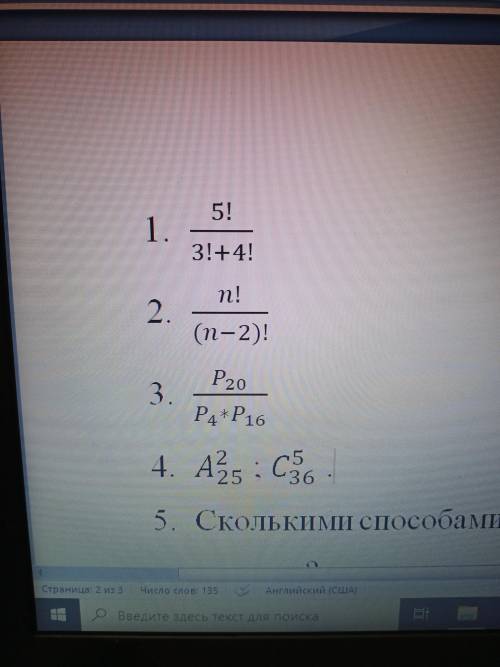
Другие вопросы по теме Математика
Популярные вопросы
- Определите координаты мест куда дед мороз отправил посылки к новому...
2 - Кчему желание короля нарушить хартию 1814 года...
1 - Выбери правильное объяснение написание окончание в слове мышка в словосочетание...
3 - 20 определите массу воздуха в комнате если плотность воздуха равна...
3 - От спинного мозга нервный импульс проводится по...
2 - 1укажите предложение с глаголом 1 спряжение а)вода в озере кажется...
2 - Методом электронного определите коэффициенты в уравнении реакции схема...
2 - Мені задали написати речення з фразеологізмами терновий вінок та макітра...
1 - Назовите синоним фразеологизма «спустя рукава»: а) через пень - колоду;...
2 - Одна из сторон параллелограмма в 3 раза больше другой найдите длину...
3
1) 5!/(3!+4!) =
Для начала, вспомним, что символ "!" в математике обозначает факториал. Факториал числа n обозначается как n! и равен произведению всех натуральных чисел от 1 до n.
Таким образом, 5! = 5 * 4 * 3 * 2 * 1 = 120.
Теперь, чтобы решить это уравнение, нам нужно вычислить факториалы чисел 3 и 4 и сложить их.
3! = 3 * 2 * 1 = 6
4! = 4 * 3 * 2 * 1 = 24
Подставим значения в исходное уравнение:
5!/(3!+4!) = 120/(6+24) = 120/30 = 4
Таким образом, ответ на это уравнение равен 4.
2) n!/((n-2)!) =
В данном уравнении нам необходимо выразить факториал числа n через факториал числа (n-2).
Сначала вспомним определение факториала:
n! = n * (n-1) * (n-2) * ... * 3 * 2 * 1
Теперь, чтобы выразить факториал числа n через факториал числа (n-2), мы можем раскрыть некоторые члены из произведения выше.
n! = n * (n-1) * (n-2) * ... * (n-(n-3)) * (n-(n-2)) * (n-(n-1)) * (n-n)!
= n * (n-1) * (n-2) * ... * (n-(n-3)) * (n-(n-2)) * (n-(n-1)) * 1
= n * (n-1) * (n-2) * ... * (n-(n-3)) * (n-(n-2)) * (n-(n-1))
Таким образом, мы видим, что факториал числа n можно записать как произведение чисел от n до (n-(n-2)).
Подставим это в исходное уравнение:
n!/((n-2)!) = (n * (n-1) * (n-2) * ... * (n-(n-3)) * (n-(n-2)) * (n-(n-1)))/[(n-2) * (n-3) * ... * 3 * 2 * 1]
= (n * (n-1) * (n-2) * ... * (n-(n-3)) * (n-(n-2)) * (n-(n-1)))/(n-2)!
Таким образом, ответ на это уравнение будет (n * (n-1) * (n-2) * ... * (n-(n-3)) * (n-(n-2)) * (n-(n-1)))/(n-2)!.
3) P_20/(P_4*P_16 ) =
В этом вопросе нам дано отношение двух перестановок.
Перестановка P_n обозначает количество способов переставить n элементов. Формула для нахождения перестановки P_n это n! (факториал числа n).
Таким образом, перестановка P_20 равна 20!
Перестановка P_4 равна 4!
Перестановка P_16 равна 16!
Подставим значения в исходное уравнение:
P_20/(P_4*P_16) = 20!/(4!*16!)
4) A_25^2 =
В этом вопросе нам дано сочетание с повторениями.
В сочетании A_n^m количество способов выбрать m элементов из n элементов, учитывая порядок (с повторениями), определяется формулой A_n^m = n^m.
Таким образом, A_25^2 = 25^2 = 625.
5) C_36^5 =
В этом вопросе нам дано сочетание без повторений.
В сочетании C_n^m количество способов выбрать m элементов из n элементов без учета порядка (без повторений), определяется формулой C_n^m = n!/(m!(n-m)!).
Таким образом, C_36^5 = 36!/(5!(36-5)!) = 36!/(5!*31!)
Это означает, что мы должны вычислить факториал числа 36 и разделить его на произведение факториалов чисел 5 и 31.
Однако, из-за большого значения факториала числа 36 и его произведения с числами 5 и 31, на данном этапе я не могу рассчитать точное число.
Надеюсь, это объяснение помогло тебе понять эти математические вопросы! Если у тебя есть дополнительные вопросы, не стесняйся задавать! Я с радостью помогу.