1. Математика
  2. 41² −39² + 37² −35² + ... +

41² −39² + 37² −35² + ... + 25² −23² (где числа 41;39;37;...;25;23 − последовательные члены арифметической прогрессии). A) 620 B) 580 C) 680 D) 640

Данил12437 Данил12437    2   14.07.2020 02:01    1

Ответы
13Sasharubakova 13Sasharubakova  15.10.2020 15:21

    41^{2}-39^{2}+37^2-35^2+...+25^2-23^2=

=(41^{2}-39^{2})+(37^2-35^2)+...+(25^2-23^2)=

=(41-39)(41+39)+(37-35)(37+35)+...+(25-23)(25+23)=

=2*(41+39)+2*(37+35)+...+2*(25+23)=

=2*(41+39+37+35+...+25+23)

В скобках сумма арифметической прогрессии.

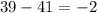
1) 39-41=-2

  d=-2

2) a_1=41;

  a_n=23

Из формулы общего члена арифметической прогрессии найдем их количество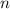 n.

a_n=a_1+(n-1)d

23=41+(n-1)*(-2)

23-41=-2(n-1)

-18=-2(n-1)

n-1=18:2

n=9+1

n=10

2) А теперь найдем значение данного выражения, заменив сумму в скобках формулой суммы n первых членов арифметической прогрессии (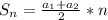S_n=\frac{a_1+a_2}{2}*n)

2*(41+39+37+35+...+25+23)=2*(\frac{41+23}{2}*10)=64*10=640

ответ:  D) 640.

ПОКАЗАТЬ ОТВЕТЫ
saule19611225 saule19611225  15.10.2020 15:21

640

Пошаговое объяснение:

Сумма равна удвоенной сумме членов арифметической прогрессии 41,39,37,..,23, которая в свою очередь равна сумме первого и последнего члена умноженному на количество членов последовательности деленное пополам.Сумма первого и последнего члена последователности равна 64, значит итоговая сумма должна делится на 64 Из предложенных вариантов подходит только 640.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
ilona125 ilona125  27.04.2022 04:37
740. Вычислите устно: П a) 1,45 + 0,15 4 + 0,8 : 0,8 6) 9,8 - 5,9 : 1,3 + 1,8 . 2 в) 30 - 0,01 + 2,4 : 0,9 : 0,1 ? r) 0,2.50 : 2,5 + 0,8 • 5 N ? ? ?...
Usimys Usimys  27.04.2022 04:50
Какие из данных точек расположены выше оси абсцисс: А(1;-2), B(-3; 5), C(4; 1), D(2; -8). 1) А и С 2) D и С 8) B и С 4) другой ответ...
Dave999 Dave999  27.04.2022 04:59
Длина отрезка АС равна 84 см. известно что BC в 6 раза длиннее AB Сколько длина отрезка AB и BC...
собакаАделет собакаАделет  27.04.2022 05:03
1 Заните формулу зависимости между величинами: А. стоимостью товара, купленного по цене 120 тг и его количеством, В расстоянием пройденым теплоходом со скоростью...
Даша222000111777 Даша222000111777  27.04.2022 05:04
327. Найдите сумму всех целых чисел: а) от -6 до 7; б) от 18 до 17; в) от 22 до 20....
dimanchik0108 dimanchik0108  27.04.2022 05:05
Решите уравнение 400:х-20=3020-х:17=3 75-х=1300:25 330+600:х=450 *...
ivanes ivanes  27.04.2022 05:05
6. Зная, что 3,1 10 3,2 , оцените: А) - 10; Б) 7-10; В) 10 — 4;...
yulik9 yulik9  27.04.2022 05:07
Решите систему уравнений :...
софи157 софи157  27.04.2022 05:07
Знайти периметр прямокутника площа якого дорівнює 14,35 м,кв а довжина3,5м...
angelinamikhay angelinamikhay  27.04.2022 05:12
Длина прямоугольника 13 см. Чему равна ширина, если периметр 42 см?...

Популярные вопросы