4. Знайти найбільше та найменше значення функцiï у = х^3 – 10х^2 + 12х – 5 на відрізку [1; 7].
Другие вопросы по теме Математика
Популярные вопросы
- Библиотеке нужно отремонтировать 800 книг. Одна мастерская может...
1 - Реши задачу при с, равном 8. В среду в магазине побывало 60 человек,...
3 - Для подключения 5 телевизоров требуется 15 м электрического шнура,...
2 - У Кости 32 солдатика, а у Вити — 46. Сколько солдатиков Витя должен...
2 - Составь и реши уравнения. 12 десятков уменьшили на неизвестное число...
2 - Вася спускался с горы 3 мин со скоростью 250 м/мин. Лёша поспорил...
3 - Из каждых 6 бросков Денис попадает в баскетбольную корзину 2 раза....
2 - Из шёлка сшили 25 сарафанов, расходуя по 3 м ткани на каждый. Сколько...
1 - От куска картона площадью 125 см2 отрезали пятую часть. Сколько...
1 - Масса трёх кружек и бидона равна массе 10 стаканов. Бидон уравновешивает...
1
ответ: max y(x) = - 2 ; min y(x) = - 77 .
[ 1 ; 7] [ 1 ; 7]
Пошаговое объяснение:
5555555555kjj uii9000iiiuiiyuh
у = х³ – 10x²+ 12х – 5 на відрізку [1; 7].
y' = ( х³ – 10x²+ 12х – 5 )' = 3x²- 20x + 12 = 3 ( x - 2/3 )( x - 6 ) .
y' = 0 ; 3 ( x - 2/3 )( x - 6 ) = 0 ; x₁ = 2/3 ∉[1; 7] ; x₂ = 6 ;
y( 1 ) = 1³ - 10* 1² + 12*1 - 5 = - 2 ;
y ( 6 ) = 6³ - 10*6² + 12*6 - 5 = - 77 ;
y ( 7 ) = 7³ - 10*7² + 12*7 - 5 = - 68 ;
max y(x) = - 2 ; min y(x) = - 77 .
[ 1 ; 7] [ 1 ; 7]
Обчислимо похідну:
Знайдемо критичні точки функції, прирівнявши похідну до нуля:
Проміжку![[1;7]](/tpl/images/2005/3696/277fc.png) належить тільки точка
належить тільки точка 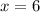 .
.
Обчислимо значення функції на кінцях проміжку, а також в знайденій критичній точці, і виберемо серед них найбільше та найменше значення.