4 корня x - 9 * 2 корня x + 8 = 0
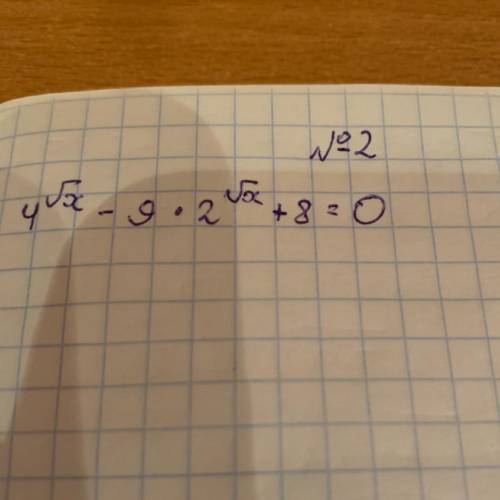
Другие вопросы по теме Математика
Популярные вопросы
- РЕШИТЬ НУЖНО РЕШИТЬ НУЖНО >...
2 - Задача на составление уравнения...
1 - Скрин задания: https://skr.sh/s2NrkcNmYNI...
3 - 1)Оптическая сила у очков соответственно равна 1,25 дптр; 4 дптр. Каковы фокусные...
1 - Ex.1 Образуй отрицательные предложения и во...
2 - Задача 1. Длина волны света в веществе равня 0.55 мкм , частота колебанийx...
2 - О каком писателе идёт речь? (Указать фамилию, имя, отчество) Одна из самых...
1 - В тексте найди слово со значением «слово, которым выражается благодарность»....
2 - решить первое задание Левый столбик решить первое задание Левый столбик >...
2 - Англиский 1-7 делать 7 класс контрольная сделайте Англиский 1-7 делать 7 класс...
1
Пошаговое объяснение:
ОДЗ:
Введём замену:
Перепишем уравнение с учётом замены:
Вернёмся к замене:
Корни удовлетворяют ОДЗ.