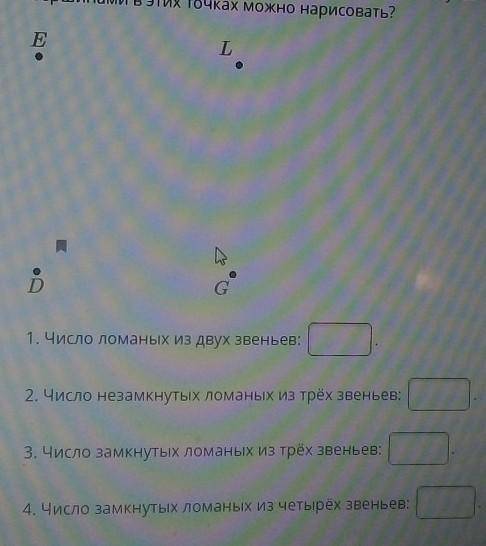
4 Даны 4 точки. Сколько разных незамкнутых и замкнутых (но не пересекающихся между собой) ломаных с вершинами в этих точках можно нарисовать? E L D G 1. Число ломаных из двух звеньев: 2. Число незамкнутых ломаных из трёх звеньев: 3. Число замкнутых ломаных из трёх звеньев: о 4. Число замкнутых ломаных из четырёх звеньев: (Подробней на фото (сам вопрос - Даны 4 точки. Сколько разных незамкнутых и замкнутых (но не пересекающихся между собой) ломаных с вершинами в этих точках можно нарисовать)

Данная задача относится к комбинаторике, а именно к задачам о перестановках и сочетаниях.

Для начала рассмотрим каждую часть задания по отдельности.

1. Число ломаных из двух звеньев:
Для создания ломаной из двух звеньев нам необходимо выбрать две точки из четырех, это можно сделать C(4, 2) = 6 способами.
Таким образом, количество ломаных из двух звеньев равно 6.

2. Число незамкнутых ломаных из трех звеньев:
Для создания незамкнутой ломаной из трех звеньев нам нужно выбрать три точки из четырех, причем они должны быть расположены в правильном порядке.
Такое выбор возможен только одним способом, так что количество незамкнутых ломаных из трех звеньев равно 1.

3. Число замкнутых ломаных из трех звеньев:
Замкнутые ломаные из трех звеньев образуются, когда все три выбранные точки не являются последовательными. Поскольку у нас есть только четыре точки, существуют только две возможности такой последовательности: ELD и ELG (D и G могут быть либо во второй, либо в третьей позиции).
Таким образом, количество замкнутых ломаных из трех звеньев равно 2.

4. Число замкнутых ломаных из четырех звеньев:
Чтобы создать замкнутую ломаную из четырех звеньев, нам нужно выбрать четыре точки из четырех, причем они должны быть расположены в правильном порядке.
Такое выбор возможен только одним способом, так что количество замкнутых ломаных из четырех звеньев равно 1.

Таким образом, ответ на вопрос:

- Число разных незамкнутых ломаных с вершинами в этих точках: 1
- Число разных замкнутых ломаных с вершинами в этих точках: 3.

Подробнее решение и изображение можно увидеть на фотографии.