3sin^2(x-3π/2)-cos(x+4π)=0
Другие вопросы по теме Математика
Популярные вопросы
- Примечание: Напишите 3 слова через запятую без нумерации. После запятой...
1 - Как переводится about ,in ,at ,with ,to ,of ,for ,on?...
2 - Вычислить определённые интегралы...
3 - Какова значимость петроглифов в наше время?...
2 - Сочинение-рассуждение (тезис,вывод,аргумент)Кем бы я хотел стать. можно...
1 - Яку кількість теплоти дістане організм якщо випити склянку чаю (250г)...
3 - Русский язык нужно как можно быстрей...
3 - Какая власть была провозглошена после Февральской революции 1917 года...
3 - Накопители на жестком диске предназначены для хранения Магнитного Временного...
2 - Найдите градусную меру угла ABC треугольника ABC если Угол ABF равен...
3
Мы можем сделать так:
Также: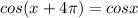
Теперь все замены подставим в уравнение и решим его:
Итого 3 решения, где k∈Z, Z - множество целых чисел
Пошаговое объяснение: