30 . в каких пределах находится отношение суммы катетов к гипотенузе в прямоугольном треугольнике? желательно с

Ответы

verinikamusia 02.10.2020 01:18

(1; √2]

Пошаговое объяснение:

Пусть a, b - катеты прямоугольного треугольника, а с - его гипотенуза.

Отношение суммы катетов к гипотенузе имеет вид:

(a + b)/c = a/c + b/c = sinα + cosα, где α - угол в исходном треугольнике (всегда острый, I четверть).

Функция у = sinα + cosα на отрезке [0; π/2] имеет максимум в точке π/4 со значением √2. Это верхний предел искомого отношения.

Нижний предел равен 1 (в точках 0 и π/2).

Таким образом, искомое соотношение лежит в пределах от 1 до √2, не достигая нижней границы интервала.

ПОКАЗАТЬ ОТВЕТЫ

спеш 02.10.2020 01:18

$(1;\sqrt{2}]$

Пошаговое объяснение:

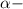$\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}=\sin\alpha+\cos\alpha=\sqrt{2}(\sin\alpha\cdot\cos\frac{\pi}{4}+\cos \alpha \cdot \sin\frac{\pi}{4})=\sqrt{2}\sin(\alpha+\frac{\pi}{4}).$

Здесь $\alpha -$ острый угол прямоугольного треугольника, то есть

$\alpha\in (0;\frac{\pi}{2})\Rightarrow t= \alpha+\frac{\pi}{4}\in(\frac{\pi}{4};\frac{3\pi}{4}).$

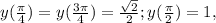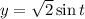Функция $y=\sin t$ возрастает на $(\frac{\pi}{4};\frac{\pi}{2}]$ и убывает на $[\frac{\pi}{2};\frac{3\pi}{4}),$ при этом $y(\frac{\pi}{4})=y(\frac{3\pi}{4})=\frac{\sqrt{2}}{2}; y(\frac{\pi}{2})=1,$ поэтому множеством значений этой функции на указанном промежутке является множество $(\frac{\sqrt{2}}{2};1],$ откуда множеством значений функции $y=\sqrt{2}\sin t$ на указанном промежутке является множество $(1;\sqrt{2}].$