3. Изобразите на координатной плоскости множество точек, координаты которых являются решениями

системы неравенств: [5]

{

² +
² ≥ 4

{ − 2 < 0

Ответы

KaapaaToown 17.11.2020 23:09

Жёлтым цветом все точки.

Пошаговое объяснение:

Я такой задачи за свои 5-9 классы не встречал :) И вот что вышло :

Система имеет вид :

$\left \{ {{x^2 + y^2 \geq 4 ,} \atop {y - 2x < 0}} \right.$

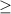x^2 + y^2 $\geq$ 4 - уравнение окружности, с радиусом большим, либо равным 2 => первая область определения двух переменных, при которой они не могут быть равными значениям внутри окружности.

y - 2x < 0 ; y < 2x - (немного непросто понять) означает, что значения переменных не могут удовлетворять прямым y = 2x и y > 2x => прямая y = 2x - означает, что значение слева прямой и самой прямой не удовлетворяют условию => чертим графики :

ответом служат все точки координатной плоскости, находящиеся правее от прямой y = 2x (желтым цветом намалякал), но не лежащие внутри окружности (но на самой могут лежать).

Областью определения является сама система :)