3.1.14 решить линейное дифференциальное уравнение
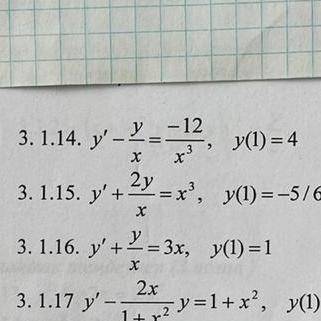
Другие вопросы по теме Математика
Популярные вопросы
- Составьте предложения со словами өнерлі, оқушы, жазушы, күнделік,...
2 - 7! составьте 6 предложений (с.п.п или с.с.п), составьте схему,...
3 - Чому пригоди дон кихот називається трагекомедією...
3 - Решите из 2 городов расстояние между которыми700км выехали одновременно...
3 - Мне завтра сдавать кровь. я утром хотела выпить кофе, но незнаю...
3 - Україні існує густа мережа повноводних річок, що належать до...
1 - „после ответ на 3 листа. чего добивается толстой композиционным...
3 - Что на русь принесло христианство? объясните, пож-та, не длинно,...
2 - Какой корень в словах: выворачивая, прослушавший, раскачка, подробность...
3 - Сочините юмористическую сказку про 7 класс....
3
замена:
общее решение
частное решение