√2cosx-sinx=√3 объясните полное решение
Другие вопросы по теме Математика
Популярные вопросы
- НУЖНО ОТВЕТИТЬ СВОИМИ СЛОВАМИ 1.Как Вы понимаете понятие «адаптивная физическая...
1 - Из пунктов А и В одновременно навстречу друг к другу выехали мотоциклист...
3 - Горизонтальная система координат связана с наблюдателем, который находится...
3 - Программирование в программе R. Расскажите что такое скрипт в программе...
1 - В приведённых примерах выбери только те, в которых один объект находится...
2 - Начерти координатный луч и отметьте на нём точки, изабражающие числа:...
3 - 2tg5x/1+tg^2(5x)=1/2 Вопрос:Скольким градусам равен наименьший положительный...
2 - В параллелограмме ABCD со сторонами АВ = 2 и AD = 5 биссектриса угла А...
1 - составить текст на английском на тему спорт с другом (родственниками,...
3 - Для куба ABCDA1B1C1D1 найдите угол между прямыми а) АС и B1D1 b) AB и...
3
Відповідь:
Покрокове пояснення:
√2cosx-sinx=√3;
Подстановка: cosx =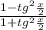 ;
;
sinx =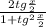
Замена:
Возвращаемся к замене: